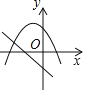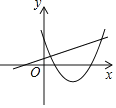Question

【题目】关于x的二次函数（k为常数）和一次函数．

（1）求证：函数的图象与x轴有交点．

（2）已知函数的图象与x轴的两个交点间的距离等于3，

①试求此时k的值．

②若，试求x的取值范围．

Answer 1

【答案】（1）见解析；（2）①k1＝1，k2＝；②当k＝1时x＜– 2或 x＞2，当k＝时，10＜x＜– 2．

【解析】

（1）证明△=b2-4ac≥0，便可得结论；
（2）①函数y1的图象与x轴的两个交点间的距离等于3，根据根与系数的关系列出k的方程，便可求解；
②分k=1和k=两种情况，依据y1＞y2列出关于x的不等式，解之可得．

解：（1）证明：△＝(2k1)2＋8 k＝4k24k＋1＋8k＝(2k＋1)2≥0，

∴函数y1＝kx2＋(2k1) x 2的图象与x轴有交点．

（2）解：①设的两根为，，则，，

，

函数的图象与轴的两个交点间的距离等于3，

，

，

解得，或；

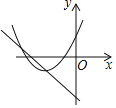
②I.当k＝1时，y1＝ x2＋ x – 2，画出y1＝ x2＋ x – 2和y2＝x＋2的图象，如图1所示，

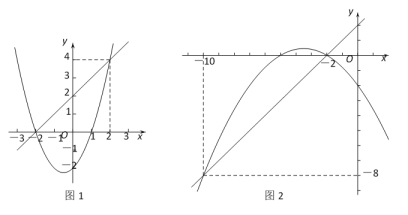
由图知，y1与y2的交点分别为(2，0)和 (2，4)，

∴当y1＞y2时x＜– 2或 x＞2；

II.当k＝时，y1＝x2x – 2，

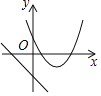
画出y1＝x2x – 2和y2＝x＋2的图象，如图2所示，

由图知，y1与y2的交点分别为(2，0)和 (10，8)，

∴当y1＞y2时10＜x＜– 2．

综上所述，当k＝1时x＜– 2或 x＞2，当k＝时，10＜x＜– 2．