题目内容
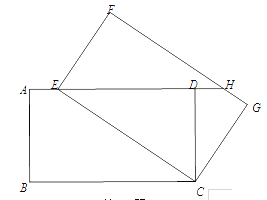
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
【答案】(1)四边形BEHC为平行四边形,证明见解析;(2)![]()
【解析】试题分析:(1)依据旋转的性质,根据AAS即可证得;(2) ①根据一组对边平行且相等的四边形是平行四边形证得四边形BEHC为平行四边形;②四边形BEHC为菱形,则△BEC是等边三角形,从而∠ABE=30°,即可得到AB与BC的比值.
试题解析:
(1) ∵矩形FECG由矩形ABCD旋转得到,
∴FE=AB=DC,∠F=∠EDC =90°,FH∥EC,∴∠FHE=∠CED,
∴△EDC≌△HFE;
(2) ①
四边形BEHC为平行四边形
∵△EDC≌△HFE,∴EH=EC,
∵矩形FECG由矩形ABCD旋转得到,
∴EH=EC=BC,EH∥BC,
∴四边形BEHC为平行四边形;
②由旋转得BC=CE
∴四边形BEHC是菱形
∴BE=CE
∴BE=BC=CE
∴△BCE是等边三角形
∴∠CBE=60°,
∵四边形ABCD是矩形
∴∠ABC=90°
∴∠ABE=30°
∵cos∠ABE=![]()
∴cos30°=![]()
∴![]()
∴当AB和BC的比值为![]() 时,四边形BEHC为菱形.
时,四边形BEHC为菱形.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目