题目内容
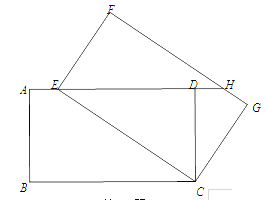
【题目】如图，在△ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点．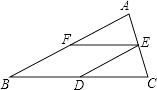 
（1）求证：四边形BDEF是菱形；
（2）若AB=12cm，求菱形BDEF的周长．
【答案】
（1）证明：∵D、E、F分别是BC、AC、AB的中点，
∴DE∥AB，EF∥BC，
∴四边形BDEF是平行四边形，
又∵DE= 
AB，EF= BC，且AB=BC，
∴DE=EF，
∴四边形BDEF是菱形
（2）解：∵AB=12cm，F为AB中点，
∴BF=6cm，
∴菱形BDEF的周长为6×4=24cm
【解析】（1）可根据菱形的定义“一组邻边相等的平行四边形是菱形”，先证明四边形BFED是平行四边形，然后再证明四边形的邻边相等即可．（2）F是AB的中点，有了AB的长也就求出了菱形的边长BF的长，那么菱形BDEF的周长也就能求出了．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对菱形的判定方法的理解，了解任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．
练习册系列答案
相关题目
