题目内容
【题目】如下图。 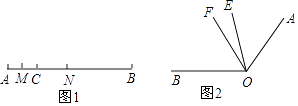
(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
【答案】
(1)解:∵M是AC的中点,AC=6,
∴MC= ![]() AC=6×
AC=6× ![]() =3,
=3,
又因为CN:NB=1:2,BC=15,
∴CN=15× ![]() =5,
=5,
∴MN=MC+CN=3+5=8,
∴MN的长为8 cm
(2)解:∵∠BOE=2∠AOE,∠AOB=∠BOE+∠AOE,
∴∠BOE= ![]() ∠AOB,
∠AOB,
∵OF平分∠AOB,
∴∠BOF= ![]() ∠AOB,
∠AOB,
∴∠EOF=∠BOE﹣∠BOF= ![]() ∠AOF,
∠AOF,
∵∠EOF=20°,
∴∠AOB=120°
【解析】(1)直接利用两点之间距离分别得出CN,MC的长进而得出答案;(2)直接利用角平分线的性质以及结合已知角的关系求出答案.
【考点精析】利用两点间的距离和角的平分线对题目进行判断即可得到答案,需要熟知同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记;从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目