Question

两个反比例函数y=

2

x

和y=

1

x

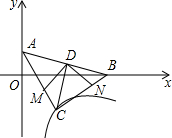
在第一象限内的图象如图所示，点P在y=

2

x

的图象上，PC⊥x轴于点C，交y=

1

x

的图象于点A，PD⊥y轴于点D，交y=

1

x

的图象于点B，当点P在y=

2

x

的图象上运动时：
（1）当PC=2时，求△AOC的面积；
（2）当点P在y=

2

x

的图象上运动时，四边形PAOB的面积是否发生变化？若不变，求出四边形PAOB的面积；若变化，请说明理由；
（3）当PA=PB时，求点P的坐标．

Answer 1

（1）S_△AOC=

1

2

|1|=

1

2

；

（2）不变，S_{四边形PAOB}=S_矩形PDOC-S_△BOD-S_△AOC=2-

1

2

-

1

2

=1；

（3）设P点坐标为：（x，y），PA=PB=a，
∵B，A在y=

1

x

的第一象限内图象上，当PA=PB时，
∴DO•DB=CO•AC，
∴y（x-a）=x（y-a），
∴x=y，
∴P点横纵坐标相等，
∴x²=2，
∴x=

2

，
∴点P的坐标为：（

2

，

2

）．