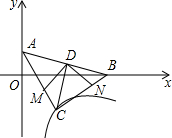
题目内容
如图,直线y=-
x+1与x轴交于B,与y轴交于A,点C在双曲线y=
上一点,且△ABC是以AB为底的等腰直角三角形,CD⊥AB于D,M、N分别是AC、BC上的一动点,且∠MDN=90°.下列结论:
①k=-4;②AM=CN;③AM2+BN2=MN2;④MN平分∠CND.
其中正确的是( )
| 1 |
| 5 |
| k |
| x |
①k=-4;②AM=CN;③AM2+BN2=MN2;④MN平分∠CND.
其中正确的是( )
| A.①②③ | B.①②④ | C.②③④ | D.①③④ |

在y=-
x+1中,令x=0,解得:y=1,则A的坐标是(0,1);
令y=0,解得:x=5,则B的坐标是(5,0),
则D的坐标是:(
,
),
设直线CD的解析式是y=5x+b,代入(
,
)得:
+b=
,解得:b=-12,
则函数的解析式是:y=5x-12,
设C的横坐标是m,则纵坐标是5m-12,
则AC的斜率是:
,BC的斜率是:
,
则
•
=-1,
解得:m=3或2.
则C的坐标是:(3,3)(舍去)或(2,-2).
把(2,-2)代入y=
得:k=-4.
故①正确;
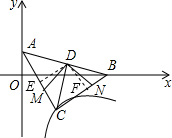 作DE⊥AC于点E,作DF⊥BC于点F.
作DE⊥AC于点E,作DF⊥BC于点F.
则DE⊥DF,且DE=DF,
∴∠DEF=∠MDN,
∴∠EDM=∠FDN,
在△DEM和△DFN中,
,
∴△DEM≌△DFN.
∴DM=DM,EM=NF,
又∵等腰直角△ABD中,CD是中线,
∴AE=CE=CF=BF,
∴AM=CN,故②正确;
∵在直角△CMN中,CM2+CN2=MN2,
设AE=CE=CF=BF=x,EM=FN=y,
则MN2=CM2+CN2=(x-y)2+(x+y)2=2(x2+y2),
AM2+BN2=(x+y)2+(x-y)2=2(x2+y2),
则AM2+BN2=MN2③正确;
当N在B点时,M正好在C点,不会出现MN平分∠CND的情况,故④一定是错误的;
故选A.
| 1 |
| 5 |
令y=0,解得:x=5,则B的坐标是(5,0),
则D的坐标是:(
| 5 |
| 2 |
| 1 |
| 2 |
设直线CD的解析式是y=5x+b,代入(
| 5 |
| 2 |
| 1 |
| 2 |
| 25 |
| 2 |
| 1 |
| 2 |
则函数的解析式是:y=5x-12,
设C的横坐标是m,则纵坐标是5m-12,
则AC的斜率是:
| 5m-13 |
| m |
| 5m-12 |
| m-5 |
则
| 5m-13 |
| m |
| 5m-12 |
| m-5 |
解得:m=3或2.
则C的坐标是:(3,3)(舍去)或(2,-2).
把(2,-2)代入y=
| k |
| x |
故①正确;
 作DE⊥AC于点E,作DF⊥BC于点F.
作DE⊥AC于点E,作DF⊥BC于点F.则DE⊥DF,且DE=DF,
∴∠DEF=∠MDN,
∴∠EDM=∠FDN,
在△DEM和△DFN中,
|
∴△DEM≌△DFN.
∴DM=DM,EM=NF,
又∵等腰直角△ABD中,CD是中线,
∴AE=CE=CF=BF,
∴AM=CN,故②正确;
∵在直角△CMN中,CM2+CN2=MN2,
设AE=CE=CF=BF=x,EM=FN=y,
则MN2=CM2+CN2=(x-y)2+(x+y)2=2(x2+y2),
AM2+BN2=(x+y)2+(x-y)2=2(x2+y2),
则AM2+BN2=MN2③正确;
当N在B点时,M正好在C点,不会出现MN平分∠CND的情况,故④一定是错误的;
故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



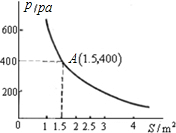 当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.
当压力不变时,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示.

 PC⊥x轴于点C,交
PC⊥x轴于点C,交