题目内容
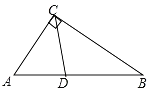
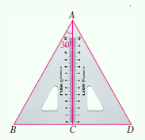
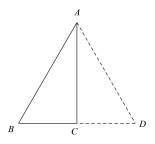
【题目】如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

交换命题的条件和结论,得到下面的命题:
在直角△ABC中,∠ACB=90°,如果![]() ,那么∠BAC=30°.
,那么∠BAC=30°.
请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.
【答案】此命题是真命题. 证明见解析.
【解析】
延长BC至点D,使得CD=BC,证AC是线段BD的垂直平分线,再证△ABD是等边三角形.得∠BAD=60°,进一步可得结论.
此命题是真命题.
证明:延长BC至点D,使得CD=BC,
∵∠ACB=90°,CD=BC
∴AC是线段BD的垂直平分线,
∴AB=AD.
∵![]() ,
,
∴BD=AB.
∴△ABD是等边三角形.
∴∠BAD=60°.
∵![]()
∴![]() =30°.
=30°.

练习册系列答案
相关题目