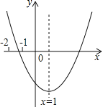
题目内容
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
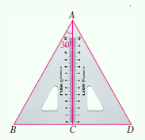
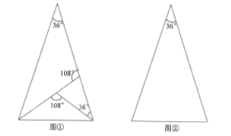
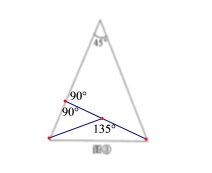
(1)图①是顶角为![]() 的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为
的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
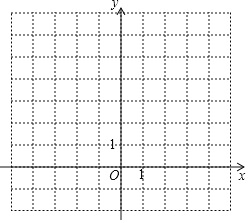
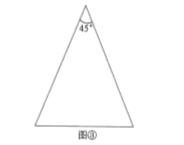
(2)图③是顶角为![]() 的等腰三角形,请你在图③中画出顶角为
的等腰三角形,请你在图③中画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
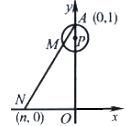
(3)![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的三分线,点
的三分线,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() ,设
,设![]() ,则
,则![]() 所有可能的值为_________.
所有可能的值为_________.
【答案】(1)见详解;(2)见详解;(3)20或40.
【解析】
(1)作底角的平分线,再作底边的平行线,即可得到三分线;
(2)过底角定点作对边的高,形成一个等腰直角三角形和一个直角三角形,然后再构造一个等腰直角三角形,即可.
(3)根据题意,先确定30°角然后确定一边为BA,一边为BC,再固定BA的长,进而确定D点,分别考虑AD为等腰三角形的腰和底边,画出示意图,列出关于x的方程,即可得到答案.
(1)如图所示:
(2)如图所示:
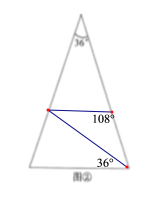
(3)①当AD=AE时,如图4,
∵![]() ,
,![]() ,
,
∴∠EDB=x°,
∴∠ADE=∠AED=2x°,
∵![]() ,
,
∴∠BAD=∠B=30°,
∴30+30=2x+x,
解得:x=20;
②当AD=DE时,如图5,
∵![]() ,
,![]() ,
,
∴∠EDB=x°,
∴∠DAE=∠AED=2x°,
∵![]() ,
,
∴∠BAD=∠B=30°,
∴30+30+2x+x=180,
解得:x=40.
③当AE=DE时,则∠EAD=∠EDA=![]() ,
,
∴∠ADC=∠EDA+∠EDC=(90-x)+x=90°
又∵∠ADC=30+30=60°,
∴这种情况不存在.
∴![]() 所有可能的值为20或40.
所有可能的值为20或40.
故答案是:20或40
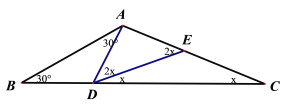
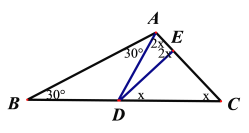
图4 图5

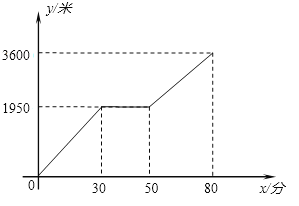
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据:
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(写两条支持你结论的理由).