题目内容
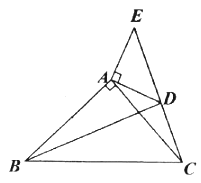
【题目】如图，一次函数y=ax+b的图象与反比例函数
的图象交于A，B两点，与X轴交于点C，与Y轴交于点D，已知
，A（n，1），点B的坐标为（﹣2，m）
（1）求反比例函数的解析式和一次函数的解析式；
（2）连结BO，求△AOB的面积；
（3）观察图象直接写出一次函数的值大于反比例函数的值时x的取值范围是 ．
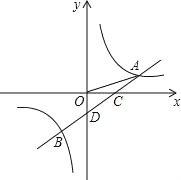
【答案】（1）y=
；y=
x﹣；（2）
；（3）﹣2＜x＜0或x＞3；
【解析】
（1）过A作AM⊥x轴于M，根据勾股定理求出OM，得出A的坐标，把A得知坐标代入反比例函数的解析式求出解析式，吧B的坐标代入求出B的坐标，吧A、B的坐标代入一次函数的解析式，即可求出解析式．
（2）求出直线AB交y轴的交点坐标，即可求出OD，根据三角形面积公式求出即可．
（3）根据A、B的横坐标结合图象即可得出答案．
解:
（1）过A作AM⊥x轴于M，
则AM=1，OA=
，由勾股定理得：OM=3，
即A的坐标是（3，1），
把A的坐标代入y=
得：k=3，
即反比例函数的解析式是y=
．
把B（﹣2，n）代入反比例函数的解析式得：n=﹣
，
即B的坐标是（﹣2，﹣），
把A、B的坐标代入y=ax+b得：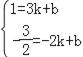
，
解得：k=
．b=﹣，
即一次函数的解析式是y=x﹣．
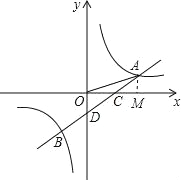
（2）连接OB，
∵y=x﹣，
∴当x=0时，y=﹣，
即OD=，
∴△AOB的面积是S△BOD+S△AOD=××2+
××3=
．
（3）一次函数的值大于反比例函数的值时x的取值范围是﹣2＜x＜0或x＞3，
故答案为：﹣2＜x＜0或x＞3．
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛，试卷题目共10题，每题10分.现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100.
整理数据：
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据：
根据以上信息回答下列问题：
（1）请直接写出表格中
，
，
，
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由（写两条支持你结论的理由）.
