��Ŀ����
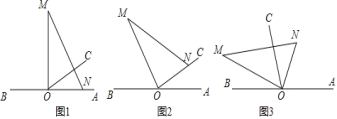
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC��![]() ����һֱ�����ǰ�
����һֱ�����ǰ�![]() ��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���
���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���![]() ______��(ֱ��д���)��
______��(ֱ��д���)��
��2����ͼ2�����ǰ�����Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��
���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�
���ٶ�����ʱ�뷽����תһ�ܣ�
�ٵ�OCת��9��ʱ����![]() �Ķ�����
�Ķ�����
���˶�������ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
���𰸡���1��6����2����45������11���25��.
��������
��1����Ϊ��AOC=30��������ON����OC����ʱ�����ǰ���ת��30������תʱ���Ϊ6s��
��2����������ת�����У����Կ�������һ����������������⣬����ON�Ƶ�O��ÿ��5�����ٶ�����ʱ�뷽����ת��ͬʱ����OCҲ��O����ÿ��10�����ٶ�����ʱ�뷽����ת��
��9��ʱ����NOC=45������OC��ת��90�������ԡ�MOC�Ķ�������45����
�ڡ�MOC=35��ʱ��Ӧ��OC��OM�غ�ǰ35�����غϺ�35������������ǣ��õ�����ʱ��������Ҫ��.
��1���ߡ�AOC=30��
�����ǰ�ÿ����ת5��
�൱ON����OC����ʱ����5t=30��
��t=6
�ʴ�Ϊ��6��
��2���ٵ�OCת��9��ʱ����COA=30��+10���9=120��
����MOA=30��+90��+5���9=165��
�֡ߡ�MOC=��MOA-��COA
������MOC=165��-120��=45��
�𣺵�OCת��9��ʱ����MOC�Ķ���Ϊ45����
����OC�˶���ʼλ��Ϊ����OP����ͼ1�����˶�t��ʱ����MOC=35����
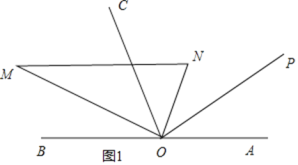
���MOP=90��+5t����COP=10t
����MOC=35��ʱ���У�90��+5t��-10t=35����10t-��90��+5t��=35��
��t=11��t=25
��Ϊ���ǰ�������OC��ֻ��תһ�ܣ����Բ������ٴ����������
�ʵ��˶�11���25��ʱ����MOC=35����