��Ŀ����
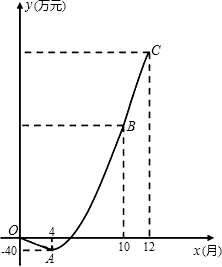
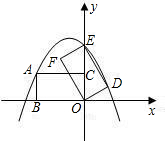
��ͼ����֪������OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=AB=2��������y=-
x2+bx+c������A��B������x���ڵ�D��E��OC�ϵĶ��㣨����C�غϣ�����EB����B����BF��BE��y����F
��1����b��c��ֵ��D������ꣻ
��2�����E��OC���˶�ʱ���ı���OEBF������������Ĺ����ԣ���֤����Ľ��ۣ�
��3������EF��BD����OE=m����BEF���BED�����֮��ΪS���ʣ���mΪ��ֵʱS��С������������Сֵ��
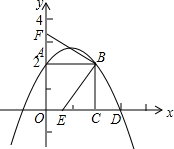
| 2 |
| 3 |
��1����b��c��ֵ��D������ꣻ
��2�����E��OC���˶�ʱ���ı���OEBF������������Ĺ����ԣ���֤����Ľ��ۣ�
��3������EF��BD����OE=m����BEF���BED�����֮��ΪS���ʣ���mΪ��ֵʱS��С������������Сֵ��
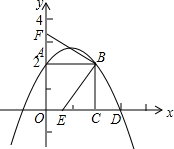
��1���ѵ�A��0��2����B��2��2������������y=-
x2+bx+c��
���b=
��c=2��
��y=-
x2+
x+2��
��-
x2+
x+2=0
���x1=-1��x2=3
��D��������3��0����
��2����E��OC���˶�ʱ���ı���OEBF��������䣻
���ı���OABC��������
��AB=BC����BCE=��BAE=��ABC=90��
�֡�BF��BE
���FBE=90��
���ABF=��CBE
���ABF�ա�BCE
���ı���OEBF�����ʼ�յ���������OABC�������
��3����ͼ��
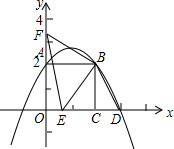
���Կ���S��BEF=S����OCBF-S��OEF-S��BEC
=
��2+2+m����2-
m��2+m��-
��2-m����2
=-
m2+m+2
S��BED=
����3-m����2
=3-m
���������ε��������СΪ0��
��3-m=-
m2+m+��
���m=2��
��
��E��OC�ϵĶ���
��m=2-
��
��m=2-
ʱS��СΪ0��
| 2 |
| 3 |
|
���b=
| 4 |
| 3 |
��y=-
| 2 |
| 3 |
| 4 |
| 3 |
��-
| 2 |
| 3 |
| 4 |
| 3 |
���x1=-1��x2=3
��D��������3��0����
��2����E��OC���˶�ʱ���ı���OEBF��������䣻
���ı���OABC��������
��AB=BC����BCE=��BAE=��ABC=90��
�֡�BF��BE
���FBE=90��
���ABF=��CBE
���ABF�ա�BCE
���ı���OEBF�����ʼ�յ���������OABC�������
��3����ͼ��
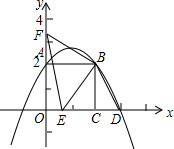
���Կ���S��BEF=S����OCBF-S��OEF-S��BEC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
S��BED=
| 1 |
| 2 |
=3-m
���������ε��������СΪ0��
��3-m=-
| 1 |
| 2 |
���m=2��
| 2 |
��E��OC�ϵĶ���
��m=2-
| 2 |
��m=2-
| 2 |

��ϰ��ϵ�д�
�����Ŀ

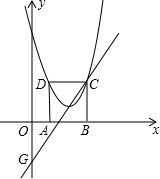
 Ӧ��Ϊ��D��������y=ax2+bx+c����A��E��D��
Ӧ��Ϊ��D��������y=ax2+bx+c����A��E��D��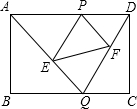 ���ֵΪ���٣�
���ֵΪ���٣�