题目内容
【题目】如图,在平面直角坐标系![]() 中,己知A(6,0),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),点C的坐标为
中,己知A(6,0),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),点C的坐标为![]() ,且
,且![]() 连接OC,AB,CD,BD.
连接OC,AB,CD,BD.
(1)写出点C的坐标为______;点B的坐标为________;
(2)当![]() 的面积是
的面积是![]() 的面积的3倍时,求点D的坐标;
的面积的3倍时,求点D的坐标;
(3)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)(2,6),(8,6);(2)D(4.5,0)或D(9,0);(3)![]() 或
或![]() .
.
【解析】
(1)先根据![]() 确定出a的值,继而求得b的值,确定出点C坐标,继而确定点B的坐标即可;
确定出a的值,继而求得b的值,确定出点C坐标,继而确定点B的坐标即可;
(2)分点D在线段OA上,点D在线段OA延长线上两种情况,结合三角形的面积公式进行求解即可得;
(3)过点D作DE∥OC,然后分点D在线段OA上,点D在线段OA延长线上两种情况分别进行求解即可.
(1) ∵![]() ,
,![]() ,
,
∴a=2,b=6,
∴C(2,6),
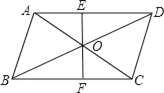
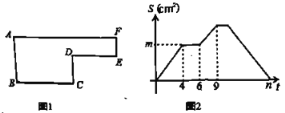
如图1,
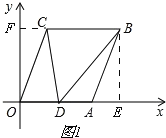
∵CB=OA,CB//OA,A(6,0),
∴BE=OF=6,FC= 2,CB=OA=6,
∴FB=2+6=8,
∴B(8,6),
故答案为: (2,6), (8,6);
(2)设![]() ,当三角形ODC的面积是三角形ABD的面积的3倍时,
,当三角形ODC的面积是三角形ABD的面积的3倍时,
①若点D在线段OA上,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
②若点D在线段OA延长线上,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上,点D的坐标为(4.5,0)或(9,0);
(3) 过点D作DE∥OC,
由平移的性质知OC∥AB,
∴OC∥AB∥DE,
∴∠OCD=∠CDE,∠EDB=∠DBA,
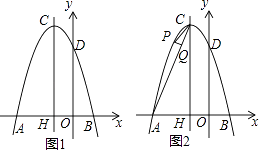
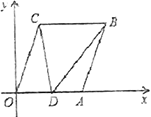
①若点D在线段OA上,(如图2),
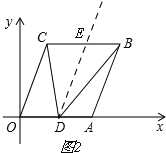
![]() ,
,
即![]() ;
;
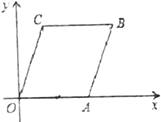
②若点D在线段OA延长线上,(如图3)
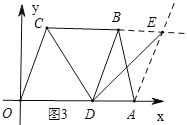
![]() ,
,
即![]() .
.

【题目】5.1劳动节,某校决定组织甲乙两队参加义务劳动,并购买队服.下面是服装厂给出的服装的价格表:
购买服装的套数 |
|
|
|
每套服装的价格 |
|
|
|
经调查:两个队共75人(甲队人数不少于40人),如果分别各自购买队服,两队共需花费5600元,请回答以下问题:
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省_________.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人),现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请写出所有的抽调方案.