Question

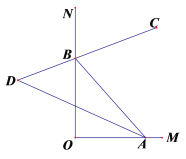
【题目】如图，∠MON=90°点A、B分别在线段OM、ON上(不与点O重合)，BC是∠ABN的平分线，BC的反向延长线与∠BAO的平分线交于点D.

(1)若∠BAO=60°，求∠ABC和∠D的度数.

(2)若∠BAO=°，求∠ABC和∠D的度数.

(3)若△ABD中有一个角是另一个角的3倍，直接写出此时∠ABC的度数.

Answer 1

【答案】⑴∠ABC=75°；∠D=45°；⑵∠ABC=45+x；∠D=45°；⑶60°或78.75°.

【解析】

(1)先求出∠ABN=150°，再根据角平分线得出∠ABC的度数，∠BAD的度数，最后由外角性质可得∠D度数即可；

(2)设∠BAD=°，利用外角性质和角平分线定义求得∠ABC=45°+ °，利用∠D=∠ABC-∠BAD即可得答案；

(3)分∠D=3∠DAB，∠DBA=3∠DAB，∠DBA=3∠D三种情况进行讨论即可.

(1)∵∠BAO=60°、∠MON=90°，

∴∠ABN=∠BAO+∠MON=150°，

∵BC平分∠ABN、AD平分∠BAO，

∴∠ABC=∠ABN=75°，∠BAD=∠BAO=30°，

∴∠D=∠CBA-∠BAD=45°；

(2)∵∠BAO=x°、∠MON=90°，

∴∠ABN=∠BAO+∠MON=(90+x)°，

∵BC平分∠ABN、AD平分∠BAO，

∴∠ABC=∠ABN=(45+x)°，∠BAD=∠BAO=x°，

∴∠D=∠CBA-∠BAD=45°；

(3)由(2)可知∠D的度数不变，∠D=45°，

若∠D=3∠DAB，则∠DAB=15°，

∵AD平分∠BAO，∴∠BAO=2∠DAB=30°，

∴∠ABN=∠BAO+∠MON=120°，

∵BC平分∠ABN，

∴∠ABC=∠ABN=60°；

若∠DBA=3∠DAB，

∵∠DBA+∠DAB=135°，

∴∠DAB=33.75°，

∵AD平分∠BAO，∴∠BAO=2∠DAB=67.5°，

∴∠ABN=∠BAO+∠MON=157.5°，

∵BC平分∠ABN，

∴∠ABC=∠ABN=78.75°；

若∠DBA=3∠D，此种情况不存在，

综上，∠ABC=60°或78.75°.