题目内容
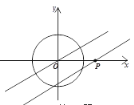
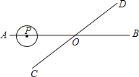
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() ,半径为
,半径为![]() 的
的![]() 的圆心在直线
的圆心在直线![]() 上,且与点
上,且与点![]() 的距离为
的距离为![]() .如果
.如果![]() 以
以![]() ∕
∕![]() 的速度,沿由
的速度,沿由![]() 向
向![]() 的方向移动,那么________秒种后
的方向移动,那么________秒种后![]() 与直线
与直线![]() 相切.
相切.
【答案】![]() 或
或![]()
【解析】
分类讨论:当点P在当点P在射线OA时⊙P与CD相切,过P作PE⊥CD与E,根据切线的性质得到PE=1cm,再利用含30°的直角三角形三边的关系得到OP=2PE=2cm,则⊙P的圆心在直线AB上向右移动了(6-2)cm后与CD相切,即可得到⊙P移动所用的时间;当点P在射线OB时⊙P与CD相切,过P作PE⊥CD与F,同前面一样易得到此时⊙P移动所用的时间.
解:
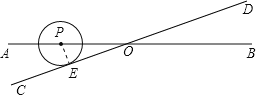
当点P在射线OA时⊙P与CD相切,如图,过P作PE⊥CD与E,
∴PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P的圆心在直线AB上向右移动了(6-2)cm后与CD相切,
∴⊙P移动所用的时间=![]() =4(秒);
=4(秒);
当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,
∴PF=1cm,
∵∠AOC=∠DOB=30°,
∴OP=2PF=2cm,
∴⊙P的圆心在直线AB上向右移动了(6+2)cm后与CD相切,
∴⊙P移动所用的时间=![]() =8(秒).
=8(秒).
故答案为4或8.

练习册系列答案
相关题目