Question

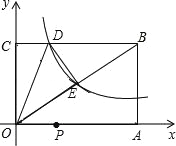
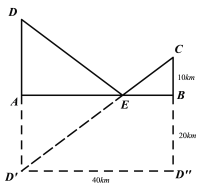
【题目】如图1，笔直的公路上有A、B两个站点相距40km，在公路的同侧有C、D两个村庄，DA⊥AB，CB⊥AB，且DA=20km，CB=10km，现政府决定在A、B之间建一个土特产加工基地E．

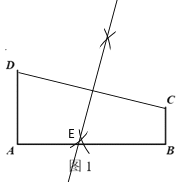
（1）若要使土特产加工基地E点到C、D两村的距离相等，请用直尺和圆规在图1中作出点E；

（2）在（1）的条件下求出基地E到A站的距离；

（3）若要使土特产加工基地E点到C、D两村的距离和（即DE +EC）最小，求出此最小的距离和．

Answer 1

【答案】（1）见解析；（2）；（3）50km

【解析】

（1）连接CD作CD的垂直平分线交AB于点E；

（2）连接DE、CE，利用线段的垂直平分线的性质得到DE=CE，再根据勾股定理建立等式求出AE；

（3）作点D关于AB的对称点，连接C，交AB于点E，(DE+CE)的最小值即为(E+EC)的值，延长CB至点，使B=A=AD=20km，则四边形AB是矩形，

利用勾股定理求出答案即可.

解：(1)如图

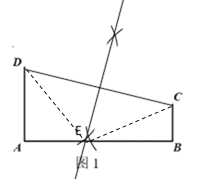
(2)连接DE、CE，

，

∴DE=CE，

，

∴,

∴,

∴AE=；

(3)作点D关于AB的对称点，连接C，交AB于点E，(DE+CE)的最小值即为(E+EC)的值，

延长CB至点，使B=A=AD=20km，则四边形AB是矩形，

∴=AB=40km，

∵BC=10km，

∴C=30km，

∴E+EC= C==50km.