题目内容
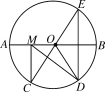
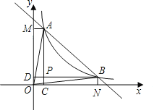
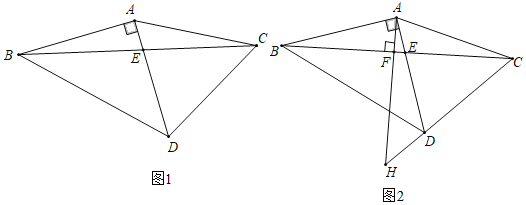
【题目】如图1,在△ABC中,AB=AC,以AB为直角边作等腰直角三角形ABD,与BC边交于点E,
(1)若∠ACE=18°,则∠ECD=
(2)探索:∠ACE与∠ACD有怎样的数量关系?猜想并证明.
(3)如图2,作△ABC的高AF并延长,交BD于点G,交CD延长线于点H,求证:CH2+DH2=2AD2.
【答案】(1)45°;(2)∠ACE=∠ACD﹣45°,理由见解析;(2)见解析
【解析】
(1)由等腰三角形的性质得出∠ABC=∠ACE=18°,得出∠BAC=180°﹣18°﹣18°=144°,由等腰直角三角形的性质得出∠BAD=90°,AB=AD,求出∠DAC=54°,证出AC=AD,由等腰三角形的性质和三角形内角和定理得出∠ACD=![]() (180°﹣54°)=63°,即可得出答案;
(180°﹣54°)=63°,即可得出答案;
(2)由(1)得出∠BAC=180°﹣2∠ACE,得出∠DAC=90°﹣2∠ACE,由等腰三角形的性质和三角形内角和定理即可得出结论;
(3)连接BH,由(2)得出∠ECD=45°,由等腰三角形的性质得出BF=CF,由线段垂直平分线的性质得出BH=CH,由等腰三角形的性质得出∠HBC=∠BCD=45°,证出∠BHC=90°,由勾股定理得出BH2+DH2=BD2.进而得出结论.
(1)∵AB=AC,
∴∠ABC=∠ACE=18°,
∴∠BAC=180°﹣18°﹣18°=144°,
∵以AB为直角边作等腰直角三角形ABD,
∴∠BAD=90°,AB=AD,
∴∠DAC=144°﹣90°=54°,
∵AB=AC,
∴AC=AD,
∴∠ACD=![]() (180°﹣54°)=63°,
(180°﹣54°)=63°,
∴∠DCE=∠ACD﹣∠ACE=63°﹣18°=45°;
故答案为:45°;
(2)∠ACE=∠ACD﹣45°;理由如下:
由(1)得:∠BAC=180°﹣2∠ACE,
∴∠DAC=∠BAC﹣90°=90°﹣2∠ACE,
∵AC=AD,
∴∠ACD=![]() (180°﹣∠DAC)=
(180°﹣∠DAC)=![]() [180°﹣(90°﹣2∠ACE)]=45°+∠ACE,
[180°﹣(90°﹣2∠ACE)]=45°+∠ACE,
∴∠ACE=∠ACD﹣45°;
(3)连接BH,如图2所示:
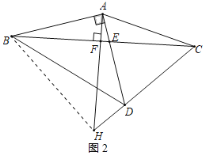
由(2)得:∠ECD=45°,
∵AB=AC,AF⊥BC,
∴BF=CF,
∴BH=CH,
∴∠HBC=∠BCD=45°,
∴∠BHC=90°,
∴BH2+DH2=BD2.
∵△ABD是等腰直角三角形,
∴BD2=2AD2,
∴CH2+DH2=2AD2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0