题目内容
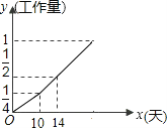
【题目】甲、乙两个工程队完成某项工程，首先是甲队单独做了10天，然后乙队加入合作，完成剩下的全部工程，设工程总量为单位1，工程进度满足如图所示的函数关系．
（1）求甲、乙两队合作完成剩下的全部工程时，工作量y与天数x间的函数关系式；
（2）求实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少多少天？
【答案】（1）y=
x-
；（2）实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少18天
【解析】
（1）根据函数图象可以设出y与x的函数解析式，然后根据图象中的数据即可求得工作量y与天数x间的函数关系式；
（2）将y=1代入（1）中的函数解析式，即可求得实际完成的天数，然后根据函数图象可以求得甲单独完成需要的天数，从而可以解答本题．
（1）设甲、乙两队合作完成剩下的全部工程时，工作量y与天数x间的函数关系式为：y=kx+b，
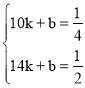，得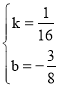
，
即甲、乙两队合作完成剩下的全部工程时，工作量y与天数x间的函数关系式是y=
x-
；
（2）令y=1，
则1=x-，得x=22，
甲队单独完成这项工程需要的天数为：1÷（
÷10）=40（天），
∵40-22=18，
∴实际完成这项工程所用的时间比由甲队单独完成这项工程所需时间少18天．
练习册系列答案
相关题目
