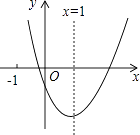Question

【题目】某鲜花销售部在春节前20天内销售一批鲜花．其中，该销售部公司的鲜花批发部日销售量y1（万朵）与时间x（x为整数，单位：天）关系为二次函数，部分对应值如表所示．

时间x（天）	0	4	8	12	16	20
销量y1（万朵）	0	16	24	24	16	0

与此同时，该销售部还通过某网络电子商务平台销售鲜花，网上销售日销售量y2（万朵）与时间x（x为整数，单位：天） 的函数关系如图所示．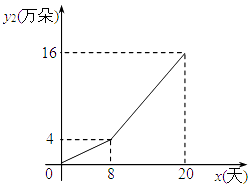

（1）求y1与x的二次函数关系式及自变量x的取值范围；
（2）求y2与x的函数关系式及自变量x的取值范围；
（3）当8≤x≤20时，设该花木公司鲜花日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时的最大值．

Answer 1

【答案】
（1）解：设y1与x的函数关系式为y1=ax2+bx+c，

，

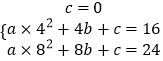解得，

，

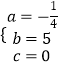即y1与x的函数关系式为y1=﹣ x2+5x（0≤x≤20）

（2）解：设当0≤x≤8时，y2=kx，

则4=8k，得k= ，

即当0≤x≤8时，y= x，

设当8＜x≤208时，y2=ax+b，

，得 ，

即当8＜x≤20时，y=x﹣4，

由上可得，y2与x的函数关系式是y2=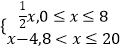

（3）解：由题意可得，

当8≤x≤20时，y=﹣ x2+5x+x﹣4= ，

∴x=12时，y取得最大值，此时y=32，

即当8≤x≤20时，第12天日销售总量y最大，此时的最大值是32万朵

【解析】（1）根据题意可以得到y1与x的二次函数关系式及自变量x的取值范围；（2）根据题意和函数图象可以得到y2与x的函数关系式及自变量x的取值范围；（3）根据（1）和（2）中的结果可以得到y与时间x的函数关系式，然后化为顶点式，从而可以解答本题．