题目内容
【题目】如图,x轴表示一条东西方向的道路,y轴表示一条南北方向的道路,小丽和小明分别从十字路口O点处同时出发,小丽沿着x轴以4千米时的速度由西向东前进,小明沿着y轴以5千米/时的速度由南向北前进.有一颗百年古树位于图中的P点处,古树与x轴、y轴的距离分别是3千米和2千米.
问:(1)离开路口后经过多少时间,两人与这棵古树的距离恰好相等?
(2)离开路口经过多少时间,两人与这颗古树所处的位置恰好在一条直线上?

【答案】(1)经过![]() 小时,两人与这棵古树的距离恰好相等;(2)离开路口经过
小时,两人与这棵古树的距离恰好相等;(2)离开路口经过![]() 小时,两人与这颗古树所处的位置恰好在一条直线上
小时,两人与这颗古树所处的位置恰好在一条直线上
【解析】
(1)设离开路口后经过x小时,两人与这棵古树的距离恰好相等.由题意得
P(2,3).A(4x,0),B(0,5x),根据PA=PB,根据勾股定理,列出方程求出![]() 即可.
即可.
(2)设离开路口经过y小时,两人与这颗古树所处的位置恰好在一条直线上.作PE⊥OB于E,PF⊥OA于F.根据B,P,A共线,得到∠BPE=∠PAF,根据tan∠BPE=tan∠PAF,列出式子求解即可.
(1)设离开路口后经过x小时,两人与这棵古树的距离恰好相等.
由题意P(2,3).A(4x,0),B(0,5x),
∵PA=PB,
∴(2﹣4x)2+32=22+(3﹣5x)2,
解得![]() 或0(舍弃),
或0(舍弃),
答:经过![]() 小时,两人与这棵古树的距离恰好相等.
小时,两人与这棵古树的距离恰好相等.
(2)设离开路口经过y小时,两人与这颗古树所处的位置恰好在一条直线上.作PE⊥OB于E,PF⊥OA于F.
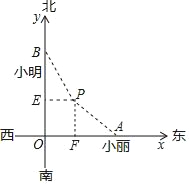
∵B,P,A共线,
∴∠BPE=∠PAF,
∴tan∠BPE=tan∠PAF,
∴![]()
解得:![]() 或0(舍弃),
或0(舍弃),
答:离开路口经过![]() 小时,两人与这颗古树所处的位置恰好在一条直线上.
小时,两人与这颗古树所处的位置恰好在一条直线上.

【题目】某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一天一共花去住宿费1510元.
普通间(元/人/天) | 豪华间(元/人/天) | 贵宾间(元/人/天) | |
三人间 | 50 | 100 | 500 |
双人间 | 70 | 150 | 800 |
单人间 | 100 | 200 | 1500 |
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一天一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是不是费用最少?为什么?