Question

【题目】如图所示，点P是∠AOB内部的一点，按要求完成下列各小题.

(1)分别画出点P关于OA、OB的对称点分别为P1、P2，连接P1P2, 分别交OA、OB于点M、N两点.

(2)连接PM，PN，若P1P2=5cm，则△PMN的周长= cm;

(3)画射线OP1与OP2，若∠AOB=55°，则∠P1OP2= °.

Answer 1

【答案】（1）作图见解析；（2）5；（3）110.

【解析】（1）如图1：

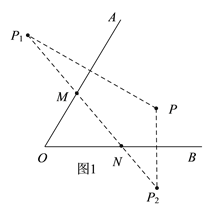
（2）如图2，∵点P与点P1关于OA对称，点P与点P2关于OB对称，

∴OA垂直平分PP1，OB垂直平分PP2，

∴P1M=PM，P2N=PN，∴C△PMN=PM+PN+MN= P1M+ P2N+MN=P1P2=5（cm）.

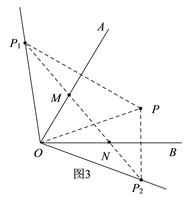
（3）如图3，连接OP，

∵点P与点P1关于OA对称，点P与点P2关于OB对称，

∴OA垂直平分PP1，OB垂直平分PP2，

∴OP1=OP，OP2=OP，

∴∠P10A=∠AOP，∠P2OB=∠BOP，

又∵∠AOP+∠BOP=∠AOB=55°，

∴∠P1OP2=∠P10A+∠P2OB+∠AOB=2∠AOB=110°.