题目内容
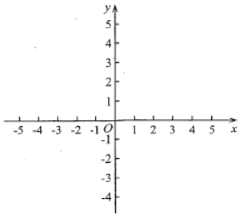
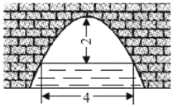
【题目】如图是一座截面边缘为抛物线的拱形桥,当拱顶离水面2米高时,水面![]() 为4米,则当水面下降1米时,水面宽度增加__________米.
为4米,则当水面下降1米时,水面宽度增加__________米.
【答案】![]()
【解析】
建立平面直角坐标系,根据题意设出抛物线解析式,利用待定系数法求出解析式,根据题意计算即可.
建立平面直角坐标系如图:

则抛物线顶点C坐标为(0,2),
设抛物线解析式y=ax2+2,
将A点坐标(﹣2,0)代入,可得:0=4a+2,
解得:a=﹣![]() ,
,
故抛物线解析式为y=﹣![]() x2+2,
x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,
也就是直线y=﹣1与抛物线相交的两点之间的距离,
将y=﹣1代入抛物线解析式得出:﹣1=﹣0.5x2+2,
解得:x=±![]() ,
,
所以水面宽度为2![]() 米,
米,
故水面宽度增加了(2![]() ﹣4)米,
﹣4)米,
故答案为:(2![]() ﹣4).
﹣4).

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案【题目】某市在九年级“线上教学”结束后,为了解学生的视力情况,抽查了部分学生进行视力检测.根据检测结果,制成下面不完整的统计图表.
被抽样的学生视力情况频数表
组别 | 视力段 | 频数 |
A | 5.1≤x≤5.3 | 25 |
B | 4.8≤x≤5.0 | 115 |
C | 4.4≤x≤4.7 | m |
D | 4.0≤x≤4.3 | 52 |
(1)求组别C的频数m的值.
(2)求组别A的圆心角度数.
(3)如果视力值4.8及以上属于“视力良好”,请估计该市25000名九年级学生达到“视力良好”的人数.根据上述图表信息,你对视力保护有什么建议?

【题目】为全面贯彻党的教育方针和落实阳光体育运动,提高青少年学生身体健康水平和体育运动水平,某校准备购买一批篮球,甲、乙两家商店的标价都是每个![]() 元,两家商店推出不同的优惠方式如下表:
元,两家商店推出不同的优惠方式如下表:
商店 | 优惠方式 |
甲 | 购买数量不超过 |
乙 | 按照标价的八折销售 |
(1)设该学校购买![]() 个篮球,在甲商店购买花费
个篮球,在甲商店购买花费![]() 元,在商店购买花费
元,在商店购买花费![]() 元,请分别求出
元,请分别求出![]() 、
、![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若学校需购买![]() 个篮球,请你通过计算进行对比,选择哪家商店更省钱?
个篮球,请你通过计算进行对比,选择哪家商店更省钱?