Question

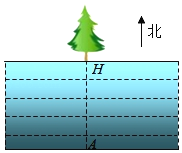
【题目】为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向．测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
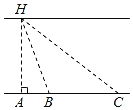
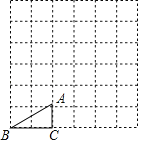
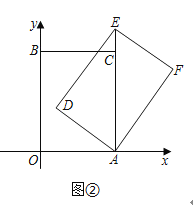
测量方案示意图
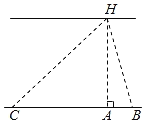
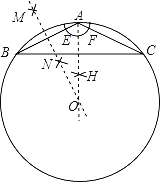
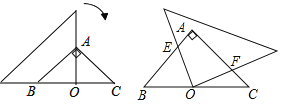
说明	点B，C在点A的正东方向	点B，D在点A的正东方向	点B在点A的正东方向，点C在点A的正西方向．
测量数据	BC＝60m， ∠ABH＝70°， ∠ACH＝35°．	BD＝20m， ∠ABH＝70°， ∠BCD＝35°．	BC＝101m， ∠ABH＝70°， ∠ACH＝35°．

（1）哪个小组的数据无法计算出河宽？

（2）请选择其中一个方案及其数据求出河宽（精确到0.1m）．（参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70）

Answer 1

【答案】（1）第二个小组的数据无法计算河宽；（2）河宽为56.4m

【解析】

（1）第二个小组的数据无法计算出河宽；

（2）第一个小组：证明BC＝BH＝60m，解直角三角形求出AH即可．

第三个小组：设AH＝xm，则CA＝，AB＝，根据CA+AB＝CB，构建方程求解即可．

解：（1）第二个小组的数据无法计算河宽；

（2）第一个小组的解法：

∵∠ABH＝∠ACH+∠BHC，∠ABH＝70°，∠ACH＝35°，

∴∠BHC＝∠BCH＝35°，

∴BC＝BH＝60m，

∴AH＝BHsin70°＝60×0.94≈56.4（m）．

第三个小组的解法：

设AH＝xm，则CA＝，AB＝，

∵CA+AB＝CB，

∴＝101，

解得x≈56.4．

答：河宽为56.4m．