题目内容
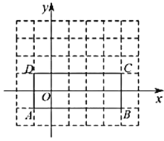
【题目】如图,在平面直角坐标系中,矩形![]() 的四个顶点坐标分别是
的四个顶点坐标分别是![]() 、
、![]() 、
、![]() 、
、![]() .函数
.函数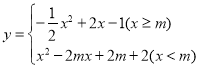 (
(![]() 为常数).
为常数).
(1)当此函数的图象经过点![]() 时,求此函数的表达式;
时,求此函数的表达式;
(2)在(1)的条件下,当![]() 时,求函数值
时,求函数值![]() 的取范围;
的取范围;
(3)当此函数的图象与矩形![]() 的边有两个交点时,直接出
的边有两个交点时,直接出![]() 的取值范围;
的取值范围;
(4)记此函数在![]() 范围内的纵坐标为
范围内的纵坐标为![]() ,若存在
,若存在![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)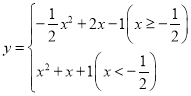 ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() ;(4)
;(4)![]() 或
或![]()
【解析】
(1)把点![]() 分别代入
分别代入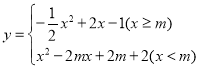 中利用待定系数法求出m的值即可;
中利用待定系数法求出m的值即可;
(2)分![]() 和
和![]() 两种情况分别求函数取值范围即可;
两种情况分别求函数取值范围即可;
(3)![]() 或
或![]() 或
或![]() ;
;
(4)![]() 或
或![]()
(1)把点![]() 代入
代入![]() 中,不成立,故
中,不成立,故![]() 的图象不经过点
的图象不经过点![]() .把点
.把点![]() 代入
代入![]() 中,得
中,得![]() ,
,
所以,当此函数的图象经过点![]() 时,此函数的表达式为
时,此函数的表达式为
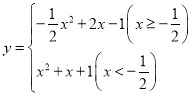 .
.
(2)当![]() 时,
时,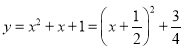 ,
,![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
综上,当![]() 时,函数值
时,函数值![]() 的取值范围是
的取值范围是![]() .
.
(3)![]() 或
或![]() 或
或![]() ;
;
(4)![]() 或
或![]()

【题目】某公司到果园基地购买某种水果慰问医务工作者,果园基地向购买超过![]() 以上(含
以上(含![]() )的客户推出两种购买方式.方式甲:价格为
)的客户推出两种购买方式.方式甲:价格为![]() 元
元![]() ,由果园基地运送到公司;方式乙:价格为
,由果园基地运送到公司;方式乙:价格为![]() 元
元![]() ,由顾客自己租车运回,从果园基地到公司的租车费用为
,由顾客自己租车运回,从果园基地到公司的租车费用为![]() 元.设该公司购买水果的数量为
元.设该公司购买水果的数量为![]() (
(![]() ).
).
(1)根据题意,填写下表:
购买水果的数量(kg) |
|
|
| … |
方式甲的总费用(元) |
| … | ||
方式乙的总费用(元) |
| … |
(2)设该公司按方式甲购买水果的总费用为![]() 元,按方式乙购买水果的总费用为
元,按方式乙购买水果的总费用为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
① 若按方式甲购买水果的总费用和按方式乙购买水果的总费用相同,则该公司购买水果的数量为 ![]() ;
;
② 若该公司购买水果的数量为![]() ,则按方式甲、方式乙中的方式 购买水果的总费用少;
,则按方式甲、方式乙中的方式 购买水果的总费用少;
③ 若该公司购买水果的总费用为![]() 元,则按方式甲、方式乙中的方式 购买水果的数量多.
元,则按方式甲、方式乙中的方式 购买水果的数量多.
【题目】甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
甲 |
|
|
| 10 |
|
乙 |
|
|
|
|
|
(1)乙种水稻5年的平均单位面积产量的平均数为______吨/公顷;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映甲种水稻5年的平均单位面积产量变化过程和趋势的统计图是______;
(3)王老汉家有100公顷田要种植水稻,你建议他种什么品种的水稻,并说明理由.