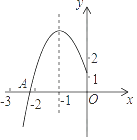题目内容
【题目】已知直线
经过点
，且与
交于点
，在
轴上存在一点
使得
的值最小，则点的坐标为_______．
【答案】
【解析】
先作点B关于x轴对称的点B'，连接AB'，交x轴于P，则点P即为所求，根据待定系数法求得直线为y=-x-2，进而得到点B的坐标以及点B'的坐标，再根据待定系数法求得直线AB'的解析式，即可得到点P的坐标．
如图所示，作点B关于x轴对称的点B'，连接AB'，交x轴于P，则点P即为所求，
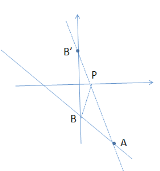
把A(2,-4）代入y=-x+b可得，b=-2，
∴直线为y=-x-2，
令x=0，则y=-2，即B(0,-2)
∴B'(0,2）
设直线AB'的解析式为y=kx+n，
把A(2,-4)，B'(0,2）代入可得，
解得
∴直线AB'的解析式为y=-3x+2，
令y=0，则x=
∴P(,0）
故答案为：(,0)
【题目】一辆经营长途运输的货车在高速公路的A处加满油后，以每小时80千米的速度匀速行驶，前往B地，如表记录的是货车一次加满油后油箱内余油量y（升）与行驶时间x（时）之间的关系：
行驶时间x/时 | 0 | 1 | 2 | 2.5 |
余油量y/升 | 100 | 80 | 60 | 50 |
则y与x的函数关系式为_____，自变量x的取值范围为_____．
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛．赛后随机抽取了其中200名学生的成绩作为样本进行整理，并制作了如下不完整的频数分布表和频数分布直方图．
成绩（分） | 频数（人） | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 20 | n |
70≤x＜80 | m | 0.15 |
80≤x＜90 | 80 | 0.40 |
90≤x＜100 | 60 | 0.30 |
请根据图表提供的信息，解答下列各题：
（1）表中m＝ ，n＝ ，请补全频数分布直方图；
（2）若用扇形统计图来描述成绩分布情况，则分数段80≤x＜90对应扇形的圆心角的度数是 ；
（3）若成绩在80分以上（包括80分）为合格，则参加这次竞赛的1500名学生中成绩合格的大约有多少名？
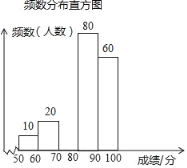
【题目】中华文明，源远流长；中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩(成绩x取整数，总分100分)作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | 40 | n |
80≤x＜90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息，解答下列问题：
(1)m＝ ，n＝ ；
(2)请补全频数分布直方图；
(3)若成绩在90分以上(包括90分)的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
