题目内容
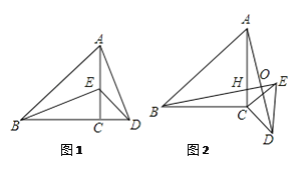
【题目】问题情境:如图1,△ABC为等腰直角三角形,∠ACB=90°,E是AC边上的一个动点(点E与A,C不重合),以CE为边在△ABC外作等腰直角△ECD,∠ECD=90°,连接BE,AD.猜想线段BE,AD之间的关系.
(1)独立思考:请直接写出线段BE,AD之间的数量关系:
(2)合作交流:城南中学八年级某学习小组受上述问题的启发,将图(1)中的等腰直角△ECD绕着点C顺时针方向旋转至如图(2)的位置,BE交AC于点H,交AD于点O.(1)中的结论是否仍然成立,请说明理由.
(3)拓展延伸:图(1)中AD和BE存在着怎样的位置关系?在等腰直角△ECD绕着点C顺时针方向旋转的过程中AD和BE的这种位置关系是否会变化?请结合图(2)说明理由.
【答案】(1)BE=AD;(2)仍成立,理由见解析;(3)成立,理由见解析
【解析】
(1)先利用边角边定理证明△BCE和△ACD全等,于是对应边BE=CD;(2)结论仍然成立,根据等腰直角三角形的性质,利用SAS定理证明△ACD≌△BCE,得对应边BE=AD;(3)因为△BCE≌△ACD,对应角∠CEB和∠CDA相等,再由同角的余角相等,可得BE⊥AD;由△BCE和△ACD全等得∠CBE=∠CAD,而∠BMC和∠AMP是对顶角,结合三角形内角和可得∠APM=90°,则BE⊥AD.
(1)解:如图(1)BE=AD,
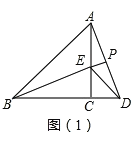
∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,CE=CD,∠BCE=∠ACD=90 ,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)不变化,理由如下:
∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,CE=DE,∠BCA=∠ECD=90°,
∴∠BCA+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD,
(3)如图,
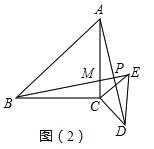
成立,理由如下:
由(1)知,△BCE≌△ACD,
∴∠CEB=∠CDA,
∵∠CBE+∠CEB=90°,
∴∠CBE+∠CDA=90°,
∴BE⊥AD,
由(2)得,∵△BCE≌△ACD,
∴∠CBE=∠CAD,
∠BMC=∠AMP,
∵∠APM=∠BCM=90°,
即BE⊥AD.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案