题目内容
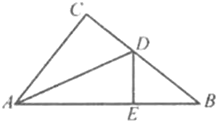
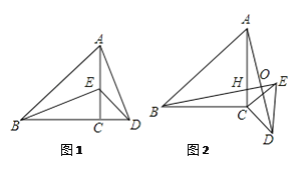
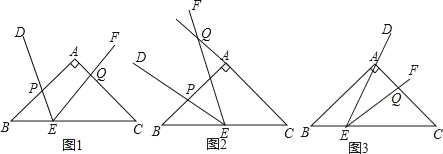
【题目】如图1，在等腰直角△ABC中，∠BAC=90°，AB=AC=2，点E是BC边上一点，∠DEF=45°且角的两边分别与边AB，射线CA交于点P，Q．
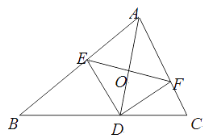
（1）如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q．设BP为x，CQ为y，试求y与x的函数关系式，并写出自变量x的取值范围；
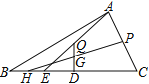
（2）如图3，点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．
【答案】（1）y=
，自变量x的取值范围是0＜x＜1；（2）在∠DEF运动过程中，△AEQ能成等腰三角形，此时BE的长为
或
．
【解析】
试题（1）先根据等腰三角形的性质及勾股定理得到∠B=∠C，
，再由
，
可证得△BPE∽△CEQ，根据相似三角形的性质可得
，设BP为x，CQ为y，即得
，从而可以求得结果；
（2）由∠AEF=∠B=∠C且∠AQE＞∠C可得AE≠AQ ，当AE=EQ时，可证△ABE≌ECQ，即可得到CE=AB=2，从而可以求得BE的长；当AQ=EQ时，可知∠QAE=∠QEA=45°，则可得AE⊥BC ，即得点E是BC的中点，从而可以求得BE的长..
（1）∵∠BAC=90°，AB=AC=2
∴∠B=∠C，
又∵，
∴∠DEB=∠EQC
∴△BPE∽△CEQ
∴
设BP为x，CQ为y
∴
∴
，自变量x的取值范围是0＜x＜1；
（2）∵∠AEF=∠B=∠C且∠AQE＞∠C
∴∠AQE＞∠AEF
∴AE≠AQ
当AE=EQ时，可证△ABE≌ECQ
∴CE=AB=2
∴BE=BC-EC=
当AQ=EQ时，可知∠QAE=∠QEA=45°
∴AE⊥BC
∴点E是BC的中点.
∴BE=
综上，在∠DEF运动过程中，△AEQ能成等腰三角形，此时BE的长为或.
