题目内容
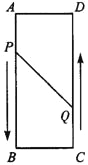
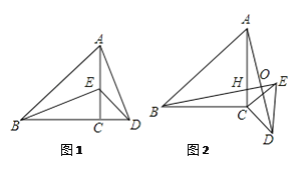
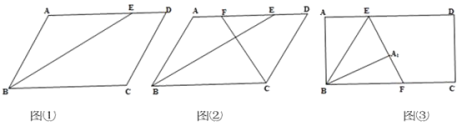
【题目】如图,城南中学八年级学习小组发现:当角平分线遇上平行线会出现等腰三角形。例如:图①,在四边形ABCD中,BE平分∠ABC,AD//BC,易得△ABE是等腰三角形。该小组将此结论作拓展:如图②,四边形ABCD中, BE平分∠BCD,CF平分∠ABC ,AD//BC,AB=CD=3,AD=4,则EF=________。如图③,如图,在长方形ABCD中,AB=3,BC=5,点E在边AD上,连接BE,△EAB沿BE翻折得到△EA1B,延长交BC于点F,若四边形EFCD的周长为11,则EF=________。
【答案】2 ![]() .
.
【解析】
②、由①结论分别得出AE和DF的长,然后根据线段之间的关系即可求出DE的长,则EF的长度可求;③过F作FG⊥ED,交ED于G,利用折叠的性质及矩形的性质推得△B A1F≌△FGE,得出EF=BF,EG= A1F,于是设EG=x,EF=y,根据勾股定理和四边形EFCD的周长为11分别列方程,联立求出y值即可;
解:②、由 ① 结论得AB=AE=4,DC=DF=3,
∴DE=AD-AE=4-3=1,EF=DF-DE=3-1=2.
③如图,过F作FG⊥ED,交ED于G,
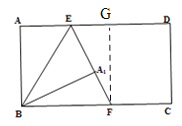
∵AB=A1B,AB=FG,
∴A1B=FG,
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠GEF=∠A1FB,
在△BA1F和△FGE中,
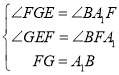 ,
,
∴△BA1F≌△FGE(AAS),
∴EF=BF,EG=A1F,
设EG=x,,EF=y,
则由EF2=EG2+FG2,
得x2+32=y2,
∵四边形EFCD的周长为11,
∴x+y+3+2(5-y)=11,
即x=y-2,
解得y=![]() .
.
故答案为:2、![]() .
.

练习册系列答案
相关题目