题目内容
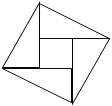
【题目】如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为( )
A.2
B.3
C.![]()
D.![]() +1
+1
【答案】A
【解析】解:延长BC至F点,使得CF=BD,
∵ED=EC,
∴∠EDC=∠ECD,
∴∠EDB=∠ECF,
在△EBD和△EFC中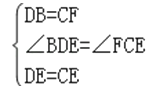
∴△EBD≌△EFC(SAS),
∴∠B=∠F
∵△ABC是等边三角形,
∴∠B=∠ACB,
∴∠ACB=∠F,
∴AC∥EF,
∴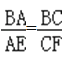 ,
,
∵BA=BC,
∴AE=CF=2,
∴BD=AE=CF=2
故选A.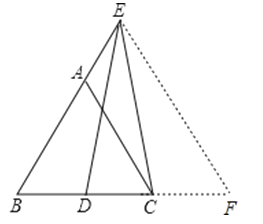
【考点精析】关于本题考查的等腰三角形的性质和等边三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
相关题目
【题目】为了解我县1800名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
等级 | A级(优秀) | B级(良好) | C级(及格) | D级(不及格) |
人数 | 22 | 28 | 18 |
根据以上提供的信息解答下列问题:
(1)若抽取的学生的数学成绩的及格率(C级及其以上为及格)为77.5%,则抽取的学生数是多少人?其中成绩为C级的学生有多少人?
(2)求出D级学生的人数在扇形统计图中的圆心角.
(3)请你估计全县数学成绩为A级的学生总人数.