题目内容
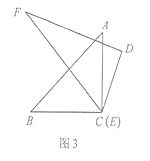
【题目】完成下面的证明,如图点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.求证:∠FDE=∠A.
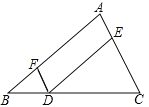
证明:∵DE∥AB,
∴∠FDE=∠ ( )
∵DF∥CA,
∴∠A=∠ ( )
∴∠FDE=∠A( )
【答案】BFD,两直线平行,内错角相等,BFD,两直线平行,同位角相等,等量代换
【解析】
根据平行线的性质得出∠FDE=∠BFD,∠A=∠BFD,推出即可;
解:证明:∵DE∥AB,
∴∠FDE=∠BFD(两直线平行,内错角相等)
∵DF∥CA,
∴∠A=∠BFD(两直线平行,同位角相等)
∴∠FDE=∠A(等量代换).
故答案为:BFD,两直线平行,内错角相等,BFD,两直线平行,同位角相等,等量代换.

练习册系列答案
相关题目