题目内容
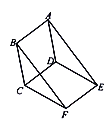
【题目】如图,已知平行四边形ABCD与平行四边形DCFE的周长相等,且![]() BAD=60°,
BAD=60°,![]() CFE=110°,则下列结论:①四边形ABFE为平行四边形;②
CFE=110°,则下列结论:①四边形ABFE为平行四边形;②![]() ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④
ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④![]() DAE=25°.其中正确的结论是.__________(填正确结论的序号)
DAE=25°.其中正确的结论是.__________(填正确结论的序号)
【答案】①②④.
【解析】
根据平行四边形的对边平行且相等即可证得AB∥CD且AB=CD,则四边形ABFE是平行四边形,根据平行四边形的对边相等以及对角相等即可得到△ADE是等腰三角形,依据等腰三角形的性质即可得证.
∵ABCD中,AB∥CD且AB=CD,
同理CD∥EF且CD=EF.
∴AB∥EF且AB=EF,
∴四边形ABFE是平行四边形.
故①正确;
∵ABCD与DCFE的周长相等,且AB=CD=EF,
∴AD=AE,即△ADE是等腰三角形.
故②正确;
∵∠BAD=60°,平行四边形ABCD中,AB∥CD,
∴∠ADC=180°-∠BAD=180°-60°=120°,
则ABCD与DCFE的角都不相等,故不全等.
故③错误;
∵DCFE中,∠CDE=∠CFE=110°,
∴∠ADE=360°-∠ADC-∠CDE=360°-120°-110°=130°,
又∵AD=DE,
∴∠DAE=![]() =25°.
=25°.
故④正确.
故答案为:①②④.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目