题目内容
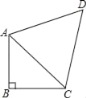
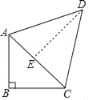
【题目】如图,∠ABC=90°,![]() ,BC=6,AD=DC,∠ADC=60°.
,BC=6,AD=DC,∠ADC=60°.
(1)求AC长.
(2)求△ADC的面积.
【答案】(1)AC=8;(2)S△ACD=16![]() .
.
【解析】
(1)根据题意,在直角三角形ABC中利用AB2+BC2=AC2,即可求得AC的长;
(2)根据AD=DC,∠ADC=60°,可知三角形ACD是等边三角形且变长为8,然后求得三角形的高,再利用三角形面积公式即可求得面积.
(1)∵∠ABC=90°,![]() ,BC=6,
,BC=6,
∴AB=![]() AC,即AB2=
AC,即AB2=![]() AC2,BC2=36,
AC2,BC2=36,
又∵AB2+BC2=AC2,
∴![]() AC2+36=AC2,36=
AC2+36=AC2,36=![]() AC2,
AC2,
∴AC=8,
(2)∵AD=DC,∠ADC=60°.
∴三角形ACD是等边三角形,
∴AD=DC=AC=8,
∴如图所示,过点D作三角形ACD的高于AC交于点E,
∴![]()
∴![]()
∴![]()

练习册系列答案
相关题目