题目内容
【题目】已知抛物线y＝x2+bx+c经过点（1，0）和点（0，3）．
（1）求此抛物线的解析式及顶点坐标；
（2）当自变量x满足﹣1≤x≤3时，求函数值y的取值范围；
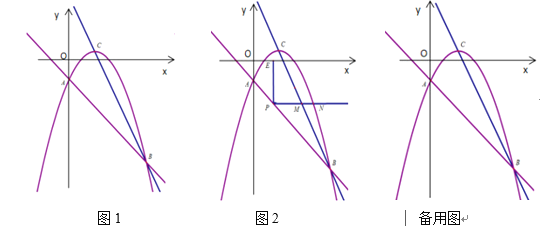
（3）将此抛物线沿x轴平移m个单位后，当自变量x满足1≤x≤5时，y的最小值为5，求m的值．
【答案】(1) 抛物线解析式为y＝x2﹣4x+3, 顶点坐标为（2，﹣1）；(2) ﹣1≤x＜8；(3) m的值为3+
或1+
【解析】
（1）利用待定系数法求抛物线解析式；然后把一般式配成顶点式得到抛物线的顶点坐标；
（2）先计算出当x＝﹣1和x＝3对应的函数值，然后根据二次函数的性质解决问题；
（3）设此抛物线沿x轴向右平移m个单位后抛物线解析式为y＝（x﹣2﹣m）2﹣1，利用二次函数的性质，当2+m＞5，此时x＝5时，y＝5，即（5﹣2﹣m）2﹣1＝5，；设此抛物线沿x轴向左平移m个单位后抛物线解析式为y＝（x﹣2+m）2﹣1，利用二次函数的性质得到2﹣m＜1，此时x＝1时，y＝5，即（1﹣2﹣m）2﹣1＝5，然后分别解关于m的方程即可．
解：（1）把（1，0），（0，3）代入y＝x2+bx+c得
解得
∴抛物线解析式为y＝x2﹣4x+3；
∵y＝x2﹣4x+3＝（x﹣2）2﹣1，
∴抛物线的顶点坐标为（2，﹣1）；
（2）当x＝﹣1时，y＝x2﹣4x+3＝8，
当x＝3时，y＝x2﹣4x+3＝0，
∴当﹣1≤x≤3时，函数值y的取值范围为﹣1≤x＜8；
（3）设此抛物线沿x轴向右平移m个单位后抛物线解析式为y＝（x﹣2﹣m）2﹣1，
∵当自变量x满足1≤x≤5时，y的最小值为5，
∴2+m＞5，即m＞3，
此时x＝5时，y＝5，即（5﹣2﹣m）2﹣1＝5，解得m1＝3+，m2＝3﹣（舍去），
设此抛物线沿x轴向左平移m个单位后抛物线解析式为y＝（x﹣2+m）2﹣1，
∵当自变量x满足1≤x≤5时，y的最小值为5，
∴2﹣m＜1，即m＞1，
此时x＝1时，y＝5，即（1﹣2﹣m）2﹣1＝5，解得m1＝1+，m2＝1﹣（舍去），
综上所述，m的值为3+或1+．
