Question

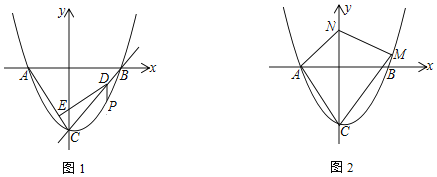
【题目】如图1，平面直角坐标系中，点O为坐标原点，抛物线交x轴于A、B两点在B的左边，交y轴于C，直线经过B、C两点．

求抛物线的解析式；

为直线BC下方的抛物线上一点，轴交BC于D点，过D作于E点设，求m的最大值及此时P点坐标；

探究是否存在第一象限的抛物线上一点M，以及y轴正半轴上一点N，使得，且若存在，求出M、N两点坐标；否则，说明理由．

Answer 1

【答案】； m的最大值为，此时点P的坐标为；存在满足条件的M、N两点，坐标分别为、

【解析】

利用直线经过B、C两点，先求出点B、C的坐标，然后利用待定系数法求出抛物线的解析式；
根据表达式，设出D点坐标，用含a的代数式分别表达出线段PD、DE，转化成m关于a的二次函数，再求m的最大值及P点坐标；
根据条件，且，利用三角形的全等去确定满足条件的M、N点，再根据函数解析式去它们的坐标．

直线经过坐标轴上B、C两点，

，

而B、C两点在抛物线上，于是有

解得，

故抛物线的解析式为．

连接AD，并延长PD交x轴于H点如图，设H点坐标为，则D点坐标为，P点坐标为，所以，

由，当时，解得或4，于是可知，且

，

由于

于是有

即：

得

即：当时，m的最大值为

此时可代入得

故m的最大值为，此时点P的坐标为

过N点分别作交CA延长线于E点，作于F点，如图2

，

而在四边形NECF中，,,,

又，且

≌,

平分

若设CM与X轴交点为G点，根据轴对称，可知G点坐标为

由、两点可得：

而点M是直线CM与抛物线的交点，于是有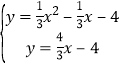

解得，或，

由此可知点M的坐标为

设N点坐标为，根据

解得，所以N点坐标为

故存在满足条件的M、N两点，坐标分别为、