��Ŀ����
����Ŀ����֪��O����O��һ��P������P������O��һ������(ֻ��Բ������ǰ������ֹ���)�������Ǽס�����ͬѧ����ҵ��
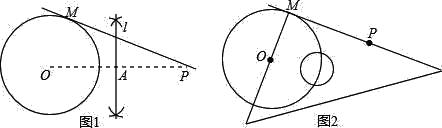
�ף�������OP����OP�Ĵ�ֱƽ����l����OP�ڵ�A��
���Ե�AΪԲ�ġ�OAΪ�뾶����������O�ڵ�M��
����ֱ��PM����ֱ��PM��Ϊ����(��ͼ1)��
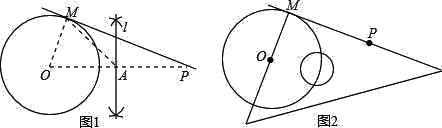
�ң�����ֱ�����ǰ��һ��ֱ�DZ�ʼ�վ�����P��
�ڵ���ֱ�����ǰ��λ�ã���������һ��ֱ�DZ߹�Բ��O��ֱ�Ƕ������ڡ�O�ϣ�����ʱֱ�Ƕ����λ��Ϊ��M��
����ֱ��PM����ֱ��PM��Ϊ����(��ͼ2)��
�������˵���ҵ������˵����ȷ����( )
A. ���Ҷ���B. ���Ҷ�����
C. �ԣ��Ҳ���D. �ײ��ԣ��Ѷ�
���𰸡�A
��������
��1������OM��OA������OP����OP�Ĵ�ֱƽ����l�ɵ�OA=MA=AP�������õ���O=��AMO����AMP=��MPA�����ԡ�OMA+��AMP=��O+��MPA=90�����ó�MP�ǡ�O�����ߣ���2��ֱ�����ǰ��һ��ֱ�DZ�ʼ�վ�����P��������һ��ֱ�DZ߹�Բ��O��ֱ�Ƕ������ڡ�O�ϣ����ԡ�OMP=90�����õ�MP�ǡ�O�����ߣ�
֤������1����ͼ1������OM��OA��
������OP����OP�Ĵ�ֱƽ����l����OP�ڵ�A����OA=AP��
���Ե�AΪԲ�ġ�OAΪ�뾶����������O�ڵ�M��
��OA=MA=AP�����O=��AMO����AMP=��MPA�����OMA+��AMP=��O+��MPA=90������OM��MP����MP�ǡ�O�����ߣ�
��2����ͼ2��
��ֱ�����ǰ��һ��ֱ�DZ�ʼ�վ�����P��������һ��ֱ�DZ߹�Բ��O��ֱ�Ƕ������ڡ�O�ϣ����OMP=90������MP�ǡ�O�����ߣ�
����λͬѧ����������ȷ��
��ѡA��

����Ŀ��ijӰԺ����25����λ����1����11����λ�����ӵ�2�ſ�ʼ��ÿһ�Ŷ���ǰһ������m����λ��
(1)�������±��Ŀո�����дһ���ʵ��Ĵ���ʽ��
��1�ŵ���λ�� | ��2�ŵ���λ�� | ��3�ŵ���λ�� | �� | ��n�ŵ���λ�� |
11 | 11+m | 11+2m | �� | ______ |
(2)��֪��18����λ���ǵ�4����λ����2������ôӰԺ���ж��ٸ���λ��