题目内容
【题目】在直角坐标系内,设A(0,0),B(4,0),C(t+4,4),D(t,4)(t为实数),记N为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则N的值可能为_____.

【答案】9或11或12
【解析】
作出平行四边形,结合图象得到平行四边形中的整数点的个数.
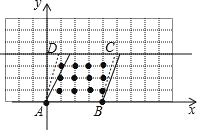
解:当t=0时,平行四边形ABCD内部的整点有:
(1,1);(1,2);(1,3);(2,1);(2,2);(2,3)(3,1);(3,2);(3,3)共9个点,
所以N(0)=9,此时平行四边形ABCD是矩形,
当平行四边形ABCD是一般平行四边形时,
将边AD,BC变动起来,结合图象得到N(t)的所有可能取值为11,12.
综上所述:N的值可能为:9或11或12.
故答案是:9或11或12.

练习册系列答案
相关题目