��Ŀ����
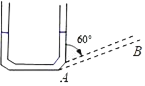
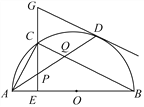
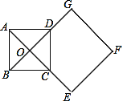
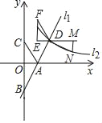
����Ŀ����ͼ��ֱ������ϵxOy�У�ֱ��11��y��tx��t��t��0���ֱ���x�ᡢy�ύ��A��B���㣬��˫����l2��y��![]() ��k��0�����ڵ�D��2��2������B��C����x��Գƣ�����AC����Rt��AOC��AD����ƽ�ƣ�ʹ��A�ƶ�����D���õ�Rt��DEF��
��k��0�����ڵ�D��2��2������B��C����x��Գƣ�����AC����Rt��AOC��AD����ƽ�ƣ�ʹ��A�ƶ�����D���õ�Rt��DEF��
��1��д��k��ֵ����A�����ꣻ
��2����F�Ƿ���l2�ϣ�����֤��Ľ��ۣ�
��3����ED���ӳ�����ȡһ��M��4��2��������M��MN��y�ᣬ��l2�ڵ�N������ND����ֱ��ND�Ľ���ʽ��
��4��ֱ��д���߶�ACɨ���������
���𰸡���1��k��4��A��1��0������2����F��l2�ϣ���3��y����![]() x+3����4���߶�ACɨ�����������ƽ���ı���ACFD�������4��
x+3����4���߶�ACɨ�����������ƽ���ı���ACFD�������4��
��������
��1�����ô���ϵ������x���ϵ�������������ɵó����ۣ�
��2����ȷ������B�����꣬�����ó���C�����꣬����ƽ�������F�����꣬�жϼ��ɣ�
��3����ȷ������N�����꣬���ô���ϵ�������ɵó����ۣ�
��4�����жϳ�ACɨ���IJ�����ƽ���ı���ACFD�����жϳ���C��D��E��һ��ֱ���ϣ�A��E��FҲ��ͬһ��ֱ���ϣ����ɽ��ۣ�
��1���ߵ�D��2��2����˫����l2��y��![]() ��k��0���ϣ�
��k��0���ϣ�
��2��![]() ��
��
��k��4
��D��2��2����ֱ��11��y��tx��t��t��0���ϣ�
��2t��t��2��
��t��2��
��ֱ��11��y��2x��2
��y��0��
��2x��2��0��
��x��1��
��A��1��0����
�ʴ�Ϊ��4����1��0����
��2����F��l2�ϣ�
�ɣ�1��֪��ֱ��l1��y��2x��2��
���B��0����2����
�ߵ�B��C����x��Գƣ�
��C��0��2����
��ƽ�ƺ�DE��AO��1��EF��CO��2��
���E��1��2������F��1��4��
��˫����l2�Ľ���ʽΪ��y��![]() ��
��
���F��1��4���������������ʽy��![]() ���ʵ�F��l2�ϣ�
���ʵ�F��l2�ϣ�
��3����M��4��2����MN��y�ᣬ��l2�ڵ�N��
���N�ĺ��������4������y��![]() �ϣ�
�ϣ�
��N��4��1����
��D��2��2����
��ֱ��ND�Ľ���ʽΪy��ax+b������a��bΪ��������a��0����
��![]() �����
����� ��
��
��ֱ��ND�Ľ���ʽΪ��y����![]() x+3��
x+3��
��4����ͼ������CF��CE��AE��
��ƽ��֪��ACɨ���IJ�����ƽ���ı���ACFD��
�ɣ�1��֪��C��0��2����E��1��2����
��D��2��2����
���C��D��E��һ��ֱ���ϣ�
ͬ��A��E��FҲ��ͬһ��ֱ���ϣ�
��ƽ��֪��EF��DE��
��F��1��4����
��AF��4��
��CD��2��
���߶�ACɨ�����������ƽ���ı���ACFD�������![]() ��CD��AF��4��
��CD��AF��4��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�