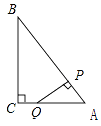题目内容
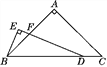
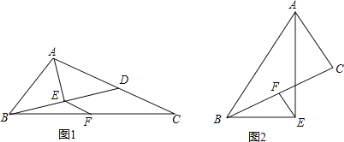
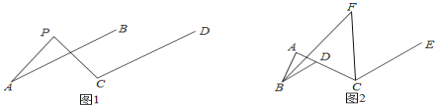
【题目】如图1,已知AB∥CD,那么图1中∠PAB、∠APC、∠PCD之间有什么数量关系?并说明理由.
如图2,已知∠BAC=80°,点D是线段AC上一点,CE∥BD,∠ABD和∠ACE的平分线交于点F,请利用(1)的结论求图2中∠F的度数.
【答案】(1)∠P=∠PCD﹣∠PAB,理由见解析;(2)∠F=40°
【解析】
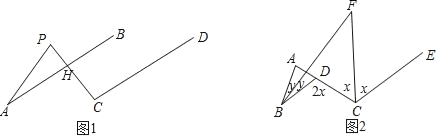
(1)先根据两直线平行得到∠PCD=∠AHC,再根据三角形的外角定理,即可得出∠P=∠PCD﹣∠PAB;(2)如图2中,设∠ABF=∠FBD=y,∠ACF=∠FCE=x,
由(1)可知:∠F=x﹣y,再根据∠BDC=∠ABD+∠A,即2x=2y+80°求得x﹣y的度数,即可求出∠F的度数.
(1)结论:∠P=∠PCD﹣∠PAB.
理由:如图1中,设AB交PC于H.
∵AB∥CD,
∴∠PCD=∠AHC,
∵∠AHC=∠PAB+∠P,
∴∠P=∠AHC﹣∠PAB,
∴∠P=∠PCD﹣∠PAB.
(2)如图2中,设∠ABF=∠FBD=y,∠ACF=∠FCE=x,
由(1)可知:∠F=x﹣y,
∵BD∥CE,
∴∠BDC=∠DCE=2x,
∵∠BDC=∠ABD+∠A,
∴2x=2y+80°,
∴x﹣y=40°,
∴∠F=40°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目