题目内容
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗
 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?9m; 81m2。
(1)篱笆只有两边,且其和为18,设一边为x,则另一边为(18-x),根据公式表示面积;据实际意义,0<x<18;
(2)根据函数性质求最值,可用公式法或配方法.
解:(1)由已知,矩形的另一边长为(18-x)m
则y=x(18-x)=-x2+18x
自变量x的取值范围是0<x<18.
(2)∵y=-x2+18x=-(x-9)2+81
∴当x=9时(0<9<18),苗圃的面积最大,最大面积是81m2.
又解:∵a=-1<0,y有最大值,
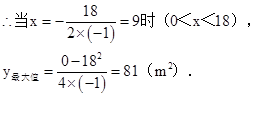

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 中,
中, 平分
平分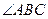 交
交 于点
于点 ,
, 平分
平分
 交
交 于点
于点 .
. ;
; ,则判断四边形
,则判断四边形 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论. 


 cm
cm
 的顶点
的顶点 在原点,点
在原点,点 的坐标为
的坐标为 ,点
,点 的纵坐标是
的纵坐标是 ,则顶点
,则顶点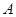 的坐标是
的坐标是 


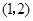

 ,则菱形较短的对角线长是( )
,则菱形较短的对角线长是( )


