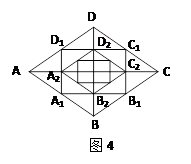
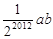题目内容
在四边形ABCD中，∠A：∠B：∠C：∠D有下列几组比值。其中能判断四边形ABCD
是等腰梯形的是
是等腰梯形的是
| A．1：2：3：4 | B．1:3:3:2 | C．1:2:2:1 | D．1：2：1：2 |
C
根据等腰梯形的判定定理可知，∠A=∠D，∠B=∠C，∠A+∠B=180°，据此进行判断．
解答：解：若∠A：∠B：∠C：∠D=1：2：3：4，四边形底角不相等，故A选项错误；
若∠A：∠B：∠C：∠D=1：3：3：2，四边形底角相等，但上底和下底不平行，故B选项错误；
若∠A：∠B：∠C：∠D=1：2：2：1，四边形ABCD是等腰梯形，故C选项正确；
若∠A：∠B：∠C：∠D=1：2：1：2，不满足等腰梯形的条件，故D选项错误．
故选C．
解答：解：若∠A：∠B：∠C：∠D=1：2：3：4，四边形底角不相等，故A选项错误；
若∠A：∠B：∠C：∠D=1：3：3：2，四边形底角相等，但上底和下底不平行，故B选项错误；
若∠A：∠B：∠C：∠D=1：2：2：1，四边形ABCD是等腰梯形，故C选项正确；
若∠A：∠B：∠C：∠D=1：2：1：2，不满足等腰梯形的条件，故D选项错误．
故选C．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
圃. 问矩形苗圃的一边长为多少时面积最大，最大面积是多少？
是四边形
的对角线
上两点，
．
．
，
，那么梯形ABCD的周长是 ．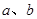
，以菱形ABCD各边的中点为顶点作矩形A1B1C1D1，然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2，……，如此下去，得到四边形A2011B2011C2011D2011的面积用含
