题目内容
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,若要使四边形EFGH为菱形,则还需增加的条件是( )
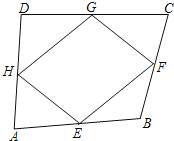
A.AC=BDB.AC⊥BDC.AC⊥BD且AC=BDD.AB=AD
【答案】A
【解析】
可添加的条件是:AC=BD,连接AC、BD,根据三角形的中位线定理得到EF∥AC,EF=![]() AC,HG∥AC,HG=
AC,HG∥AC,HG=![]() AC,推出EF=HG,EF∥HG,即可得四边形EFGH是平行四边形,再根据三角形的中位线定理得到EF=
AC,推出EF=HG,EF∥HG,即可得四边形EFGH是平行四边形,再根据三角形的中位线定理得到EF=![]() AC,GF=
AC,GF=![]() BD,由AC=BD,推出EF=GF,进而证明四边形EFGH为菱形.
BD,由AC=BD,推出EF=GF,进而证明四边形EFGH为菱形.
可添加的条件是:AC=BD,
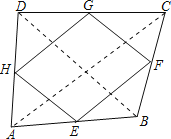
证明:连接AC、BD,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴EF∥AC,EF=![]() AC,HG∥AC,HG=
AC,HG∥AC,HG=![]() AC,GF=
AC,GF=![]() BD,
BD,
∴EF=HG,EF∥HG,
∴四边形EFGH是平行四边形.
∵AC=BD,
∴EF=GF,
∴四边形EFGH为菱形.
故选:A.

【题目】某果品超市经销一种水果,已知该水果的进价为每千克15元,通过一段时间的销售情况发现,该种水果每周的销售总额相同,且每周的销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的关系如表所示:
(元)的关系如表所示:
每千克售价 | 25 | 30 | 40 |
每周销售量 | 240 | 200 | 150 |
(1)求出每周销售量![]() (千克)与每千克售价
(千克)与每千克售价![]() (元)的函数关系式.
(元)的函数关系式.
(2)由于销售淡季即将来临,超市要完成每周销售量不低于300千克的任务,则该种水果每千克售价最多定为多少元?
(3)在(2)的基础上,超市销售该种水果能否达到每周获利2000元?说明理由.
【题目】下表,是池州市今年“五一”这周内日最高气温的统计表,关于这7天的日最高气温的众数,中位数,方差分别是:( )
日期 | 29日 | 30日 | 5月1日 | 2日 | 3日 | 4日 | 5日 |
日最高气温 | 16°C | 19°C | 22°C | 24°C | 26°C | 24°C | 23°C |
A. 24,23,10B. 24,23,![]() C. 24,22,10D. 24,22,
C. 24,22,10D. 24,22,![]()