题目内容
【题目】现有一笔直的公路连接![]() 、
、![]() 两地,甲车从
两地,甲车从![]() 地驶往
地驶往![]() 地,速度为每小时60千米,同时乙车从
地,速度为每小时60千米,同时乙车从![]() 地驶往
地驶往![]() 地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往
地,速度为每小时80千米.途中甲车发生故障,于是停车修理了2.5小时,修好后立即开车驶往![]() 地.设甲车行驶的时间为
地.设甲车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() .已知
.已知![]() 与
与![]() 的函数关系的部分图像如图所示.
的函数关系的部分图像如图所示.
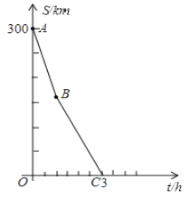
(1)直接写出![]() 点的实际意义.
点的实际意义.
(2)问:甲车出发几小时后发生故障?
(3)将![]() 与
与![]() 的函数图象补充完整.(请对画出的图象用数据作适当的标注)
的函数图象补充完整.(请对画出的图象用数据作适当的标注)
【答案】(1)是甲车故障开始修理了,乙车还在继续行驶;(2)1小时;(3)见解析
【解析】
(1)B点开始两车距离变化变慢,说明甲车故障开始修理了;
(2)根据图象,3小时时两车相遇,再求出相遇时甲车行驶的路程,然后根据时间=路程÷速度计算即可得解;
(3)根据两车行驶的情况分类讨论.
解:(1)点![]() 的实际意义是甲车故障开始修理了,乙车还在继续行驶;
的实际意义是甲车故障开始修理了,乙车还在继续行驶;
(2)t=3时,两车距离为0km,两车相遇,
∵80×3=240km,
∴发生故障前甲车行驶路程为300-240=60km,
时间位:60÷60=1小时;
∴甲车出发1小时后发生故障.
(3)甲车再次行驶时,t=1+2.5=3.5h,
乙车到达N地时,t=300÷80=3.75h,
甲车到达M地时,t=300÷60+2.5=7.5h,
所以,3<t≤3.5时,s=80(t-3)=80t-240,
t=3.5时,80t-240=80×3.5-240=40km,
3.5<t≤3.75时,s=80(t-3)+60(t-3.5)=140t-450,
t=3.75时,140t-450=140×3.75-450=75km,
3.75<t≤7.5时,s=60(t-3.75)+75=60t-150
补全图形如图所示.

练习册系列答案
相关题目