题目内容
【题目】综合题。
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,AE与DH交于O,若AE=DH,求证:AE⊥DH;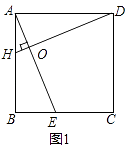
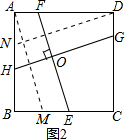
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,EF与GH交于O,若EF=HG,探究线段EF与HG的位置关系,并说明理由;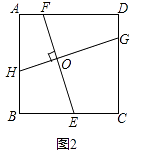
(3)如图3所示,在(2)问条件下,若HF∥GE,试探究线段FH、线段EG与线段EF的数量关系,并说明.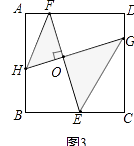
【答案】
(1)
证明:∵四边形ABCD是正方形,
∴AB=DA,∠ABE=90°=∠DAH.
∴∠HAO+∠OAD=90°.
∵AE⊥DH,
∴∠ADO+∠OAD=90°.
∴∠HAO=∠ADO,
在△ABE和△DAH中 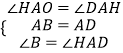 ,
,
∴△ABE≌△DAH(ASA),
∴AE=DH
(2)
解:EF⊥GH.
理由:如图2,将FE平移到AM处,则AM∥EF,AM=EF.
将GH平移到DN处,则DN∥GH,DN=GH.
∵EF=GH,
∴AM=DN,
在Rt△ABM和Rt△DAN中, ![]() ,
,
∴Rt△ABM≌Rt△DAN,
∴∠BAM=∠ADN,
∵∠DAM+∠BAM=90°,
∴∠DAM+∠ADN=90°,
∴AM⊥DN,
∴EF⊥HG
(3)
解:EG+FH= ![]() EF.理由:如图3,
EF.理由:如图3,
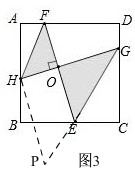
过点H作HP∥FE交GE的延长线于P,
∵FH∥EG,
∴四边形EFHP是平行四边形,
∴FH=PE,HP=EF,
由(2)知,EF=HG,
∴HP=HG,
∵HP∥FE,EF⊥HG,
∴HP⊥HG,
在Rt△PHG中,根据勾股定理得,PG= ![]() HG=
HG= ![]() EF,
EF,
∵PG=EG+PE=EG+FH,
∴EG+FH= ![]() EF
EF
【解析】(1)由正方形的性质得AB=DA,∠ABE=90°=∠DAH.所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO,于是△ABE≌△DAH,可得AE=DH;(2)将FE平移到AM处,则AM∥EF,AM=EF,将GH平移到DN处,则DN∥GH,DN=GH.再判断出Rt△ABM≌Rt△DAN,最后代换即可得出结论;(3)先构造出平行四边形EFHP,得出FH=PE,HP=EF,再用勾股定理即可得出结论.

【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?





