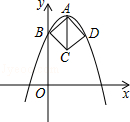题目内容
【题目】如图21所示,海岛上有A,B两个观测点,点B在点A的正东方,海岛C在观测点A的正北方,海岛D在观测点B的正北方,从观测点A看海岛C,D的视角∠CAD与从观测点B看海岛C,D的视角∠CBD相等,那么海岛C,D到观测点A,B所在海岸的距离相等吗?为什么?

【答案】相等,理由见解析.
【解析】
设AD,BC相交于点O,由于∠CAD=∠CBD,∠COA=∠DOB, 得∠C=∠D.
再根据∠CAB=∠DBA=90°,∠C=∠D, AB=BA,可判定△CAB≌△DBA,根据全等三角形的性质可得: CA=DB.
解:相等.理由:设AD,BC相交于点O.
∵∠CAD=∠CBD,∠COA=∠DOB,
∴由三角形内角和定理,得∠C=∠D.
由已知得∠CAB=∠DBA=90°.
在△CAB和△DBA中,∠C=∠D,∠CAB=∠DBA,AB=BA,
∴△CAB≌△DBA(AAS),
∴CA=DB,
∴海岛C,D到观测点A,B所在海岸的距离相等.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目