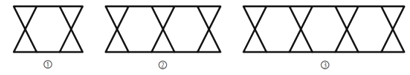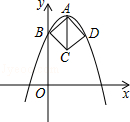题目内容
【题目】如图24①,点A,B,C,D在同一直线上,AB=CD,作EC⊥AD于点C,FB⊥AD于点B,且AE=DF.
(1)求证:EF平分线段BC;
(2)若将△BFD沿AD方向平移得到图②时,其他条件不变,(1)中的结论是否仍成立?请说明理由.

【答案】(1)见解析;(2)见解析.
【解析】
(1)现根据CE⊥AD,BF⊥AD,可得∠ACE=∠DBF=90°,由于AB=CD,
所以AB+BC=BC+CD,即AC=DB,在Rt△ACE和Rt△DBF中,
![]() ,可证Rt△ACE≌Rt△DBF,继而可得CE=FB,
,可证Rt△ACE≌Rt△DBF,继而可得CE=FB,
在Rt△CEG和Rt△BFG中,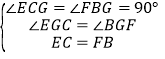 ,可证Rt△CEG≌Rt△BFG,
,可证Rt△CEG≌Rt△BFG,
可得CG=BG,即EF平分线段BC.
(2)先根据CE⊥AD,BF⊥AD,可得∠ACE=∠DBF=90°,由于AB=CD,可得AB-BC=CD-BC,即AC=DB,在Rt△ACE和Rt△DBF中,![]() ,可证Rt△ACE≌Rt△DBF,可得CE=FB,
,可证Rt△ACE≌Rt△DBF,可得CE=FB,
在Rt△CEG和Rt△BFG中,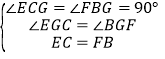 ,可证Rt△CEG≌Rt△BFG,
,可证Rt△CEG≌Rt△BFG,
可得CG=BG,即EF平分线段BC.
(1)因为CE⊥AD,BF⊥AD,
所以∠ACE=∠DBF=90°,
因为AB=CD,
所以AB+BC=BC+CD,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
所以Rt△ACE≌Rt△DBF,
所以CE=FB,
在Rt△CEG和Rt△BFG中,
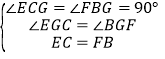 ,
,
所以Rt△CEG≌Rt△BFG,
所以CG=BG,即EF平分线段BC.
(2)(1)中结论成立,理由为:
因为CE⊥AD,BF⊥AD,
所以∠ACE=∠DBF=90°,
因为AB=CD,
所以AB-BC=CD-BC,即AC=DB,
在Rt△ACE和Rt△DBF中,
![]() ,
,
所以Rt△ACE≌Rt△DBF,
所以CE=FB,
在Rt△CEG和Rt△BFG中,
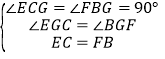 ,
,
所以Rt△CEG≌Rt△BFG,
所以CG=BG,即EF平分线段BC.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案