题目内容
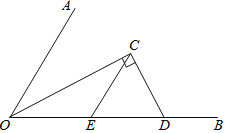
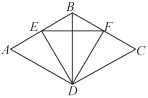
【题目】如图,把等边三角形ABD和等边三角形BCD拼合在一起,点E在AB边上移动,且满足AE=BF,试说明不论点E怎样移动,△EDF总是等边三角形.
【答案】见解析.
【解析】
根据等边三角形性质得出BD=AD,∠CBD=∠A=60°,∠ADB=60°,根据SAS推出△EAD≌△FBD,推出DE=DF,∠ADE=∠BDF,求出∠EDF=60°,根据等边三角形的判定推出即可.
解:∵△ABD和△BCD是等边三角形,
∴BD=AD,∠CBD=∠A=∠ADB=60°,
在△EAD和△FBD中,
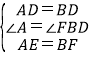 ,
,
∴△EAD≌△FBD,
∴DE=DF,∠ADE=∠BDF,
∴∠EDF=∠BDF+∠BDE=∠ADE+∠BDE=∠ADB=60°,
又∵DE=DF,
∴△EDF是等边三角形.

练习册系列答案
相关题目