Question

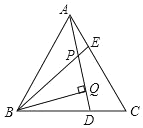
【题目】如图①，在四边形ABCD中，AC⊥BD于点E，AB=AC=BD，点M为BC中点，N为线段AM上的点，且MB=MN.

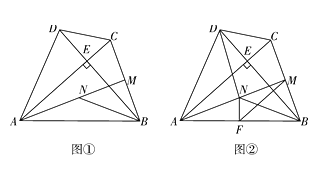
（1）求证：BN平分∠ABE；

（2）若BD=1，连结DN，当四边形DNBC为平行四边形时，求线段BC的长；

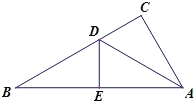
（3）如图②，若点F为AB的中点，连结FN、FM，求证：△MFN∽△BDC.

Answer 1

【答案】（1）证明见解析；（2）；（3）证明见解析.

【解析】（1）由AB=AC知∠ABC=∠ACB，由等腰三角形三线合一知AM⊥BC，从而根据∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC，再由△MBN为等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°可得证；

（2）设BM=CM=MN=a，知DN=BC=2a，证△ABN≌△DBN得AN=DN=2a，Rt△ABM中利用勾股定理可得a的值，从而得出答案；

（3）F是AB的中点知MF=AF=BF及∠FMN=∠MAB=∠CBD，再由即可得证．

（1）∵AB=AC，

∴∠ABC=∠ACB，

∵M为BC的中点，

∴AM⊥BC，

在Rt△ABM中，∠MAB+∠ABC=90°，

在Rt△CBE中，∠EBC+∠ACB=90°，

∴∠MAB=∠EBC，

又∵MB=MN，

∴△MBN为等腰直角三角形，

∴∠MNB=∠MBN=45°，

∴∠EBC+∠NBE=45°，∠MAB+∠ABN=∠MNB=45°，

∴∠NBE=∠ABN，即BN平分∠ABE；

（2）设BM=CM=MN=a，

∵四边形DNBC是平行四边形，

∴DN=BC=2a，

在△ABN和△DBN中，

∵，

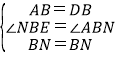∴△ABN≌△DBN（SAS），

∴AN=DN=2a，

在Rt△ABM中，由AM2+MB2=AB2可得（2a+a）2+a2=1，

解得：a=±（负值舍去），

∴BC=2a=；

（3）∵F是AB的中点，

∴在Rt△MAB中，MF=AF=BF，

∴∠MAB=∠FMN，

又∵∠MAB=∠CBD，

∴∠FMN=∠CBD，

∵，

∴，

∴△MFN∽△BDC．