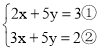题目内容
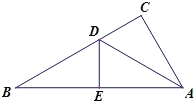
【题目】如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
【答案】(1)△ABC是直角三角形;(2)CD长为3.
【解析】
(1)利用勾股定理的逆定理判断得出即可;
(2)设CD=x,则DE=x,BD=8﹣x,在Rt△BDE中,根据DE2+BE2=BD2列出方程,进而求出即可.
(1)△ABC是直角三角形.
理由:在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8﹣x.
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+(10-6)2=(8﹣x)2,
∴x2+16=64﹣16x+x2,
∴x=3,即CD长为3.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目