题目内容
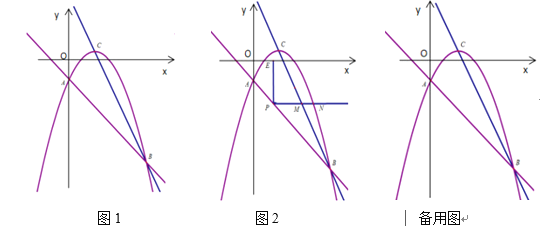
【题目】如图,直线![]() 与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,且点A在y轴上,抛物线的顶点C的坐标为![]() .
.
(1)求抛物线的解析式;
(2)点P是线段AB上一动点,射线![]() 轴并与直线BC和抛物线分别交于点M、N,过点P作
轴并与直线BC和抛物线分别交于点M、N,过点P作![]() 轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使
轴于点E,当PE与PM的乘积最大时,在y轴上找一点Q,使![]() 的值最大,求
的值最大,求![]() 的最大值和此时Q的坐标;
的最大值和此时Q的坐标;
(3)在抛物线上找一点D,使△ABD为直角三角形,求D点的坐标.
【答案】(1)![]() ;(2)
;(2) ![]() ,Q点坐标为
,Q点坐标为![]() ;(3)
;(3) ![]() 点坐标为
点坐标为![]()
【解析】
(1)直线![]() 与抛物线分别交于点A、点B,求出点A的坐标,根据抛物线的顶点C的坐标为
与抛物线分别交于点A、点B,求出点A的坐标,根据抛物线的顶点C的坐标为![]() .设出抛物线的解析式,把点A的坐标代入即可求出抛物线的解析式.
.设出抛物线的解析式,把点A的坐标代入即可求出抛物线的解析式.
(2) 联立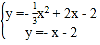 ,求出点B的坐标,用待定系数法求出BC的解析式为
,求出点B的坐标,用待定系数法求出BC的解析式为![]() ,设
,设![]() ,则
,则![]() ,进而表示出
,进而表示出![]() ,根据二次函数的性质即可求出它的最大值,此时
,根据二次函数的性质即可求出它的最大值,此时![]() ,即可求出
,即可求出![]() 的最大值以及此时Q的坐标.
的最大值以及此时Q的坐标.
(3)根据△ABD为直角三角形,分成三种情况进行讨论即可.
(1) 由题意得:![]()
![]() ,
,
设抛物线解析式为![]()
将点![]() 代入得:
代入得:![]()
解得:![]() ,
,
![]() ,
,
![]() .
.
(2) 联立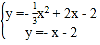 解得:
解得:![]() 或
或![]()
即![]() 点的坐标为
点的坐标为![]()
设![]() 的解析式为
的解析式为![]() ,代入
,代入![]() 和
和![]() 得:
得:

![]() 解得:
解得:![]()
∴BC的解析式为![]()
设![]() ,则
,则![]()
![]() ,
,
![]()
∴![]() ,即
,即![]()
∵C、P在y轴同侧
∴Q在PC延长线上时,![]() 最大,
最大,![]()
此时,Q为直线PC与y轴的交点,
由![]() 和
和![]() 得直线PC的解析式为:
得直线PC的解析式为:![]()
∴Q点坐标为![]()
(3) ![]() 点坐标为
点坐标为![]()

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目