题目内容
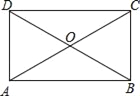
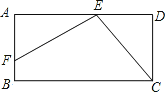
【题目】如图,已知矩形ABCD中,E是AD上一点,F是AB上的一点,EF⊥EC,且EF=EC.
(1)求证:△AEF≌△DCE.
(2)若DE=4cm,矩形ABCD的周长为32cm,求AE的长.
【答案】(1)证明见解析;(2)6cm.
【解析】(1)根据EF⊥CE,求证∠AEF=∠ECD.再利用AAS即可求证△AEF≌△DCE.
(2)利用全等三角形的性质,对应边相等,再根据矩形ABCD的周长为32cm,即可求得AE的长.
(1)证明:∵EF⊥CE,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,
∴∠AEF=∠ECD.
在Rt△AEF和Rt△DEC中,
∠FAE=∠EDC=90°,∠AEF=∠ECD,EF=EC.
∴△AEF≌△DCE.
(2)解:∵△AEF≌△DCE.
AE=CD.
AD=AE+4.
∵矩形ABCD的周长为32cm,
∴2(AE+AE+4)=32.
解得,AE=6(cm).
答:AE的长为6cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)