Question

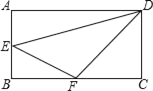
【题目】如图，在长方形ABCD中，AB＝4cm，BC＝8cm．E、F分别是AB、BC的中点．则E到DF的距离是_____cm．

Answer 1

【答案】3

【解析】

根据矩形的性质得出CD=AB=4cm，AD=BC=8cm，∠A=∠B=∠C=∠D=90°，由已知条件求出AE、BE、BF、CF的长，根据勾股定理求出DF，求出△DEF的面积，作EG⊥DF于G，由三角形的面积求出EG即可．

解：∵四边形ABCD是矩形，

∴CD＝AB＝4cm，AD＝BC＝8cm，∠A＝∠B＝∠C＝∠D＝90°，

∵E、F分别是AB、BC的中点，

∴AE＝BE＝ AB＝2cm，BF＝CF＝ BC＝4cm，

∴DF＝ ＝4 （cm），

∴△DEF的面积＝矩形ABCD的面积﹣△BEF的面积﹣△CDF的面积﹣△ADE的面积

＝8×4﹣ ×4×2﹣ ×4×4﹣ ×8×2

＝12（cm2），

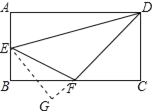
作EG⊥DF于G，如图所示：

则△DEF的面积＝ DFEG＝12，

∴EG＝ ＝3 （cm），

即E到DF的距离是3 cm，

故答案为：3 ．